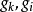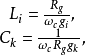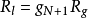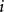基本介紹
基於低通原型濾波器的綜合設計方法得到的表格和曲線是設計實際濾波器的基礎,但不能直接套用,這是因為實際濾波器與低通原型濾波器存在兩方面的差異:一是衰減特性和頻率尺度不同,二是元件的數值和性質的不同。因此,要利用低通原型濾波器的設計表格和曲線來設計實際的濾波器,首先須將實際濾波器的衰減特性通過頻率變換,成為低通原型濾波器的衰減特性;然後查找低通原型濾波器的表格和曲線,求得低通原型濾波器的歸一化元件值,再利用等衰減條件和頻率變換,求出實際濾波器的歸一化元件值;最後進一步求出實際濾波器的真實元件值。
可見,要利用低通原型濾波器的現成設計表格和曲線求實際濾波器的真實元件值,既要用到
頻率變換又要用到
等衰減條件。所謂頻率變換,就是將低通原型的衰減特性的(角)頻率變數
變換為實際濾波器的(角)頻率變數
,而等衰減條件則可藉助圖1所示的兩個結構相似的梯形網路導出。圖中兩種結構的信源內阻和負載均為純電阻,且其值不隨頻率的變化而變化。在圖1(a)中,信源角頻率為
,梯形網路各支路的阻抗為
;在圖1(b)中,信源角頻率為
,各支路阻抗為
,如果這兩個梯形網路各支路的阻抗一一相等。即
 圖1(a)等衰減條件原理圖-低通原型濾波器
圖1(a)等衰減條件原理圖-低通原型濾波器 圖1(b)等衰減條件原理圖-實際濾波器
圖1(b)等衰減條件原理圖-實際濾波器根據等衰減條件下的頻率變換,即可通過低通原型濾波器的歸一化元件值分別求得四類濾波器的真實元件值。下面介紹低通原型濾波器向低通濾波器、高通濾波器的頻率變換。
低通濾波器
實際低通濾波器真實元件值的確定可按以下四個步驟進行。
(a)頻率變換
設實際的和原型的低通濾波器的頻率變數分別為
和
,兩者的衰減特性如圖2所示。要求在頻率為
的點上分別對應於
,兩者的衰減量L彼此
(b)查圖表和曲線得到低通原型的歸一化元件值。
(c)求實際低通濾波器的歸一化元件值
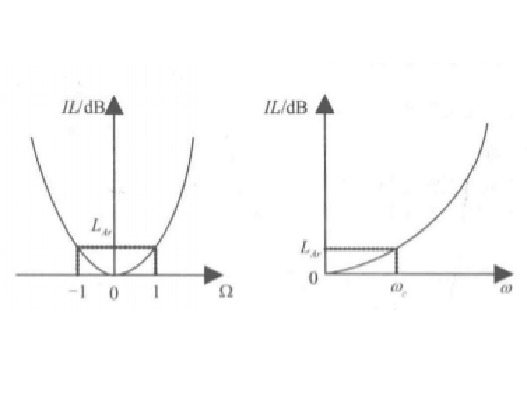
 圖2(a) 實際低通濾波器的頻率特性
圖2(a) 實際低通濾波器的頻率特性 圖2(b) 低通原型濾波器的頻率特性
圖2(b) 低通原型濾波器的頻率特性圖3(a)和(b)分別示出了原型的和實際的低通濾波器的電路結構,欲使這兩種濾波器有相等的衰減特性,根據式(1),應有
式中,下標k為串聯元件標號,i為並聯元件標號,它們分別取奇數和偶數。由此得到實際低通濾波器的歸一化元件值為
(d)求實際低通濾波器的真實元件值
求實際低通濾波器的真實元件值,只需對信源內阻
進行反歸一化即可得到
和
,即
而實際負載則由原型電路的負載性質確定。若
並聯。則
以上討論的是電感輸入式電路的情況,對電容輸入式電路,上述分析同樣適用,只是串聯元件標號k與並聯元件標號
互換。此外,確定實際低通濾波器真實元件值的步驟同樣適用於其他三類濾波器。
高通濾波器
藉助於頻率變換,可將低通原型濾波器的頻率特性轉換為高通濾波器的頻率特性。此時,可採用以下的頻率變換函式:
式中,
為高通濾波器的頻率變數,
為低通原型的頻率變數,兩者的衰減頻率特性分別如圖3(a)和(b)所示。這樣,基於等衰減條件,即可由低通原型濾波器設計表格中查出的歸一化元件值
,通過轉換得到電感輸入式低通原型電路對應的高通濾波器電路的歸一化電感
和電容
值。高通濾波器電路結構中的電感和電容將取代電感輸入式低通原型濾波器電路中的並聯電容和串聯電感的位置,
和
(仍記為
)的值應按以下公式計算:
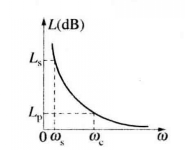 圖3(a) 高通濾波器的頻率特性
圖3(a) 高通濾波器的頻率特性 圖3(b) 低通原型的頻率特性
圖3(b) 低通原型的頻率特性 圖3 (c) 對應於電感輸入式低通原型的電路
圖3 (c) 對應於電感輸入式低通原型的電路式中,
分別為低通原型濾波器電路中的電感和電容對應的g值。通過電感輸入式低通原型電路轉換得到的對應高通濾波器電路如圖3(c)所示。
這樣,實際的電感輸入式高通濾波器的電路結構中的電感和電容的真實元件值分別為
類似地,對電容輸入式低通原型轉換得到的高通濾波器,其對應電路同樣可根據電容輸入式低通原型濾波器電路畫出,而其歸一化電感和歸一化電容值以及對應的真實值與低通原型的歸一化元件值之間同樣滿足上述關係,只是需將相關參數的下標
和
互換。
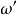
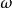
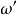

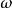

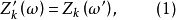
 圖1(a)等衰減條件原理圖-低通原型濾波器
圖1(a)等衰減條件原理圖-低通原型濾波器 圖1(b)等衰減條件原理圖-實際濾波器
圖1(b)等衰減條件原理圖-實際濾波器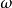
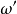
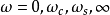


 圖2(a) 實際低通濾波器的頻率特性
圖2(a) 實際低通濾波器的頻率特性 圖2(b) 低通原型濾波器的頻率特性
圖2(b) 低通原型濾波器的頻率特性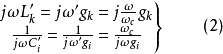
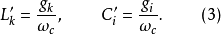
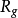
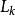
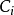
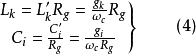
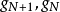
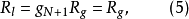
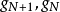
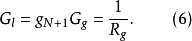
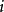
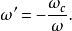
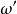
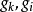
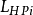

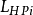

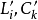
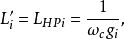
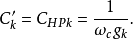
 圖3(a) 高通濾波器的頻率特性
圖3(a) 高通濾波器的頻率特性 圖3(b) 低通原型的頻率特性
圖3(b) 低通原型的頻率特性 圖3 (c) 對應於電感輸入式低通原型的電路
圖3 (c) 對應於電感輸入式低通原型的電路