簡介
項名達(1789~1850),中國清代數學家,原名萬準,字步萊,號梅侶,浙江錢塘(今杭州市)人,祖籍安徽歙縣。生於乾隆五十四年,卒於道光三十年。嘉慶二十一年(1816)為舉人,考授國子監學正,道光六年(1826)成進士,改任知縣,但未就職。應考進士期間,曾在京盤桓數年,與友人研討數學,後返居故里。道光十七年(1837)前,主講苕南。此後,在杭州著名的三大書院之一
紫陽書院執教,並研究數學。道光二十六年(1846)冬,退職還家,集中精力撰著書稿,主要數學著作有《象數一原》6卷(1849),《勾股六術》1卷(1825),《三角和較術》1卷(1843),《開諸乘方捷術》1卷(1845),後三種合刻為《下學庵算術》印行。
人物成就
他在數學方面的著名成就之一是“橢圓求
周術”,這個結果和現在中學課本“微積分初步”中求平面曲線弧長的微積分方法一致。另外,項名達和
戴煦共同發現了指數為有理數的二項定理。項名達還在概括和推廣清代數學家、天文學家安圖證出的正弦、正矢的冪級數展開式等的計算中,得到了有關三角函式冪級數展開式的兩個新公式。
他所著作的《象數一原》的主要內容是論述三角函式冪級數展開式問題,他撰寫此書時已年老病重,僅寫成整分起度弦矢率論、半分起度弦矢率論、零分起度弦矢率論(兩卷)、諸術通詮、諸術明變,共6卷。其中卷四和卷六未能完稿,由其友人
戴煦遵從他的囑託於鹹豐七年(1857)補寫完成,並為橢圓求
周術補作圖解1卷,故現傳本《象數一原》共 7卷。在此書中,他推廣了明安圖和董祐誠(1791~1823)的結果。董祐誠同明安圖一樣,也用連比例的方法討論了全弧與分弧所對的弦的關係以及全弧和分弧的中矢(即該弧所張的弓形的高),得到四個冪級數公式。項名達進一步歸納為下列兩個公式:設сn和сm分別為圓內某弧с的
n倍和m倍弧長,
vn和
vm分別為相應的中矢,
r為圓半徑,則有 (圖一):
 圖一
圖一由這兩個公式可推導出明安圖的九個公式和董祐誠的四個公式,其中包括正弦和反正弦的冪級數展開式、正矢和反正矢的冪級數展開式以及圓周率π 的無窮級數表達式等。
項名達的另一項成就是求出橢圓周長公式(圖二):式中
p為橢圓周長,
e為橢圓離心率,
α與
b為橢圓長半軸與短半軸。這是中國在二次曲線研究方面最早的重要成果。
 圖二
圖二他還據此推出圓周率倒數公式(圖三):
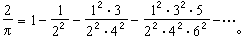 圖三
圖三項名達與
戴煦還共同討論求二項式
n次根的簡法,在《開諸乘方捷術》中提出了冪指數為 1/
n的二項式定理以及用逐次逼近法開
n次方的遞推公式(圖四):
 圖四
圖四按上述公式逐次求得的αk+1,即為準確到不同程度的近似值。《勾股六術》與《三角和較術》內容淺顯易懂,是項名達為初學者撰寫的數學入門書。在這兩卷書中,對於勾股形、平面三角形及球面三角形的各邊及其和、差的互求關係,做了較系統的分類與總結。
史籍記載
項名達,字梅侶,仁和人。嘉慶二十一年舉人,考授國子監學正。道光六年,成進士,改官知縣,不就,退而專攻算學。三十年,卒於家,年六十有二。著述甚富,今傳世者,但有下學庵句股六術及圖解,復附句股形邊角相求法三十二題,合為一卷。以句股和較相求諸題術稍繁難,爰取舊術稍為變通。分術為六,使題之相同者通為一術,釐然悉有以御之。第一、二、三術及第四術之前二題,悉本舊解,餘為更定新術,皆別注捷法,各為圖解,以明其意。第四、五、六術其原皆出於第三術,可釋之以比例。第三術以句弦較比股,若股與句弦和,以股弦較比句,若句與股弦和,是為三率連比例。凡有比例加減之,其和較亦可互相比例。故第四、五、六術諸題,皆可由第三術之題加減而得,即可因第三術之比例而另生比例。因比例以成同積,而諸術開方之所以然遂明。名達又創有弧三角總較術,求橢員弧線術,術定,未有詮釋,以義奧趣幽,難猝竟事,故六術獨先成雲。
名達與烏程
陳杰、錢塘
戴煦契最深,晚年詣益精進,謂古法無用,不甚涉獵,而專意於平弧三角,與傑意不謀而合。與傑論平三角,名達曰:“平三角二邊夾一角,逕求斜角對邊,向無其法,竊嘗擬而得之,君聞之乎?”傑曰:“未也。”錄其法以歸。蓋以甲乙邊自乘與甲丙邊自乘相加,得數寄左;乃以半徑為一率,甲角餘弦為二率,甲乙、甲丙兩邊相乘倍之為三率,求得四率,與寄左數相減,鈍角則相加,平方開之,得數即乙丙邊。
又嘗謂泰西杜德美之割圜九術,理精法妙,其原本於三角堆,
董方立定四術以明之,洵為卓見。惟求倍分弧,有奇無偶,
徐有壬補之,庶幾詳備。名達嘗玩三角堆,嘆其數祗一遞加,而理法象數,包蘊無窮,夫方圜之率不相通,通方圜者必以尖,句股,尖象也;三角堆,尖數也。古法用半徑屢求句股得圜周,不勝其繁。杜氏則以三角堆御連比例諸率,而弧弦可以互通,割圜術蔑以加矣。然以此制八線全表,每求一數,必乘除兩次,所用弧線,位多而乘不便,董、徐二氏大、小弧相求法亦然。向思別立簡易法,因從三角堆整數中推出零數,但用半徑,即可任求幾度分秒之正餘弦,不煩取資於弧線及他弧弦矢。且每一乘除,便得一數,似可為制表之一助。
又著象數原始一書,未竟,疾革時,囑
戴煦。後煦索稿於名達子錦標,校算增訂六閱月而稿始定,都為七卷。原書之四,僅六紙,並第七卷皆煦所補也。卷一曰整分起度弦矢率論,卷二曰半分起度弦矢率論,卷三、卷四曰零分起度弦矢率論,皆以兩等邊三角形明其象,遞加法定其數,末乃申論其算法。卷五曰諸術通詮,取新立弧弦矢求他弧弦矢二術、半徑求弦矢二術及杜、董諸術,按術詮釋之。卷六曰諸術明變,雜列所定弦矢求八線術,開諸乘方捷術,算律管新術,橢員求
周術,以明皆從遞加數轉變而得。卷七曰橢員求周圖解,原術以袤為徑,求大員周及周較,相減而得周,補術則以廣為徑,求小員周,周較相加而得周,末系以圖解。
徐有壬巡撫江蘇,郵書索煦寫定本梓行,刻甫就而有壬殉難,書與板皆毀焉。
有王大有者,字吉甫,
仁和諸生。翰林院待詔。窮究天算,問業於處士
戴煦。凡煦所著述,皆錄副本去,名達見之,因與煦訂交。大有嘗校割圜捷術合編。後殉於杭州。
 圖一
圖一 圖二
圖二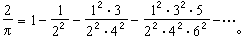 圖三
圖三 圖四
圖四 圖一
圖一 圖二
圖二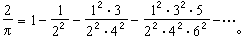 圖三
圖三 圖四
圖四