靴襻法,也可以稱之為自助法(Bootstrap Method,Bootstrapping或自助抽樣法)是一種從給定訓練集中有放回的均勻抽樣,也就是說,每當選中一個樣本,它等可能地被再次選中並被再次添加到訓練集中。當樣本來自總體,能以常態分配來描述,其抽樣分布(Sampling Distribution)為常態分配(The Normal Distribution);但當樣本來自的總體無法以常態分配來描述,則以漸進分析法、自助法等來分析。採用隨機可置換抽樣(random sampling with replacement)。對於小數據集,自助法效果很好。
基本介紹
- 中文名:靴襻法,自助法
- 外文名:Bootstrap Method
- 學科:計算機
- 定義:一種從訓練集中有放回的均勻抽樣
- 有關術語:抽樣
- 領域:數據分析
- 目的:選出符合要求的數據
靴襻法,自助法簡介,抽樣,抽樣過程,抽樣方法,自助法在藥物經濟學評價中的套用,Bootstrap 分析,計算步驟,套用實例,
靴襻法,自助法簡介
靴襻法,自助法由Bradley Efron於1979年在《Annals of Statistics》上發表。是以自助採樣(bootstrap sampling)為基礎。給定包含m個樣本的數據集D,我們對它進行採樣產生數據集 D′:每次隨機從D中挑選出一個樣本,將其拷貝放入D′, 然後再將該樣本放回初始數據集D中,使得該樣本在下次採樣時仍有可能被採樣到;這個過程重複執行m次後,我們就得到可包含m個樣本數據的數據集D′,這就是自助採樣的結果.樣本在m次採樣中始終不被採到到機率為

由此可知通過自助採樣,初始數據集D中約有36.8%的樣本未出現在採樣數據集D′中。於是我們可將D′ 用作訓練集,D∖D′用作測試集。
優缺點:自助法在數據集較小,難以有效劃分訓練/測試集時很有用,但是,自助法改變了初始數據集的分布,這會引入估計偏差,所以在數據量足夠時,一般採用留出法和交叉驗證法。
抽樣
在統計學中,抽樣(Sampling)是一種推論統計方法,它是指從目標總體(Population,或稱為母體)中抽取一部分個體作為樣本(Sample),通過觀察樣本的某一或某些屬性,依據所獲得的數據對總體的數量特徵得出具有一定可靠性的估計判斷,從而達到對總體的認識。
抽樣過程
抽樣過程主要包括以下幾個階段:
定義總體(母體)
確定抽樣框
確定抽樣方法
決定樣本量
實施抽樣計畫
抽樣與數據收集
回顧抽樣過程
抽樣方法
簡單隨機抽樣(simple random sampling),也叫純隨機抽樣。從總體N個單位中隨機地抽取n個單位作為樣本,使得每一個容量為樣本都有相同的機率被抽中。特點是:每個樣本單位被抽中的機率相等,樣本的每個單位完全獨立,彼此間無一定的關聯性和排斥性。簡單隨機抽樣是其它各種抽樣形式的基礎。通常只是在總體單位之間差異程度較小和數目較少時,才採用這種方法。
系統抽樣(systematic sampling),也稱等距抽樣。將總體中的所有單位按一定順序排列,在規定的範圍內隨機地抽取一個單位作為初始單位,然後按事先規定好的規則確定其他樣本單位。先從數字1到k之間隨機抽取一個數字r作為初始單位,以後依次取r+k、r+2k……等單位。這種方法操作簡便,可提高估計的精度。
分層抽樣(stratified sampling)。將抽樣單位按某種特徵或某種規則劃分為不同的層,然後從不同的層中獨立、隨機地抽取樣本。從而保證樣本的結構與總體的結構比較相近,從而提高估計的精度。
整群抽樣(cluster sampling)。將總體中若干個單位合併為組,抽樣時直接抽取群,然後對中選群中的所有單位全部實施調查。抽樣時只需群的抽樣框,可簡化工作量,缺點是估計的精度較差。
自助法在藥物經濟學評價中的套用
在藥物經濟學研究中, 國外學者在利用可信區間法進行敏感度分析時,常用的方法有 Fieller 理論、 Taylor 公式和靴襻法(bootstrap method ) 分析。其中 Fieller 理論、Taylor 公式在計算成本 - 效果比的可信區間時要求成本和效果數據的分布滿足常態分配,而實際上臨床試驗所得到的數據多數不服從常態分配,因此利用它們來計算增量成本 - 效果比的可信區間有一定的局限性。而 bootstrap 分析對數據的分布不作任何要求, 因而套用範圍更廣 。
Bootstrap 分析
下面以樣本均值方差的 bootstrap 分析來說明其基本思想:
首先假定 X (  ) 是樣本大小為 n 、來自於均值為μ且方差為
) 是樣本大小為 n 、來自於均值為μ且方差為 的同一樣本總體的一個抽樣。假如用F表達樣本總體的累積分布,則有 F ( x ) =Pr (
的同一樣本總體的一個抽樣。假如用F表達樣本總體的累積分布,則有 F ( x ) =Pr (  ) ,這意味著每一
) ,這意味著每一  是一具有累積分布 F 的隨機變數,可簡記為
是一具有累積分布 F 的隨機變數,可簡記為  ~ F 。在實際中,經常假定樣本總體服從高斯分布。此時,其樣本均值的方差為:
~ F 。在實際中,經常假定樣本總體服從高斯分布。此時,其樣本均值的方差為:






當 未知時,由統計理論可知,樣本方差的估計為
未知時,由統計理論可知,樣本方差的估計為


以上是對樣本總體服從常態分配而言的,對於服從其他分布的樣本總體,則很少有這樣的解析解。樣本均值方差估計的是具有同一總體分布 F 的各樣本間的均值的變化。對於理想的情況, 假設有許多來自於同一總體的 F 的樣本,則就不需要用如上所述的的估計式來估計方差, 因為此時可以直接從這許多的樣本中求得均值, 然後由所得的均值求取方差。由於受到各種各樣因素的影響,很難得到許多來自於同一分布的樣本。然而,儘管不可能得到來自於同一分布 F 的總體的許多樣本,但可以從近似於分布 F 的總體中獲得樣本。這就是 bootstrap 方法的基本思想,它用一個可重複抽樣的分布 F 的估計代替未知的因而不能重複抽樣的分布 F 。
計算步驟
在藥物經濟學中, 將上述變數 “均值方差” 改為 “增量成本 - 效果比” 即可進行敏感度分析。計算步驟如下:① 產生與每組記錄數相同個數的隨機數, 按照隨機數對各組進行有放回的隨機抽樣, 組成一個 boots 樣本; ② 對該樣本進行增量成本效果分析, 得到一個增量成本效果值;③ 重複產生 boots 樣本,並計算增量值,循環 n 次( 一般 n>250 次) ;④對 n 個增量成本值進行排序,得到 5% 下限值和 95% 上限值。
套用實例
本研究運用 bootstrap 分析對兩種三聯療法治療幽門螺桿菌( HP ) 感染的消化性潰瘍方案進行藥物經濟學評價。
治療方案的選擇:根據我院臨床實際治療抗 HP 感染的消化性潰瘍情況,並參考有關文獻, 分別選擇以膠體鉍( CBS )為基礎的方案( BMA 三聯療法)和以質子泵抑制劑( PPI )為基礎的方案( LMC 三聯療法) 。
病例選擇: 選擇經採用 Giemsa 染色法, 尿素酶試驗、13 C 或 14 C- 尿素呼吸試驗等檢測HP 陽性的消化性潰瘍門診患者 186 例,其中十二指腸潰瘍 155 例, 胃潰瘍 31 例;年齡26~ 70 歲,平均 41 歲; 潰瘍直徑 5~ 20 mm ,數目 ≤2個,1 周內未接受鉍劑和抗生素治療,未服用非甾類抗炎藥或皮質激素,排除複合性潰瘍、 幽門梗阻、 活動性出血和心、 肺、 肝、 腎功能損害。186 例隨機分成兩組: A 組 96 例,男 70 例,女 26例,平均年齡( 42± 8 ) 歲;B 組 90 例, 男 62 例,女 28 例,平均年齡(40± 8 ) 歲。兩組患者臨床主要症狀( 疼痛、 反酸、 燒心、 噯氣、 腹脹等) 比較差異無統計學意義。停藥 4 周后複查胃鏡,觀察潰瘍癒合情況, 重複檢查 HP 。
檢測方法及判斷:兩種方案在對 HP 的檢測及判斷方面基本相同, 其檢測方法採用 Giemsa 染色法、尿素酶試驗、13 C 或 14 C- 尿素呼吸試驗等,幾種檢測方法均具有準確性。在HP 陽性及陰性的判斷上也以 2 項檢測方法具有相同的結果為準。
治療方法: A 組( 採用 BMA 三聯療法) :枸櫞酸鉍鉀片( 德諾) 240 mg 、 阿莫西林片 500 mg 、 甲硝唑片 400 mg , 均每日2 次, 連用 2 周。 B 組( 採用 LMC 三聯療法) :蘭索拉唑 30 mg ,甲硝唑 400 mg ,克拉黴素 500 mg,均每日 2 次,連用 1 周。
成本確定:為使分析結果具有一定的參考意義, 所有費用均按 2004 年我院的實際價格計算。檢驗成本:Giemsa 染色法 20 元 / 次,快速尿素酶試驗 20元 /次,H13 C 或 14 C- 尿素呼吸試驗檢測130 元 / 次,每位受試者按實際檢測次數計算檢驗成本。藥物成本:A 組單日成本 12.49 元,療程 14 d ;B 組單日成本 77.48 元,療程 7 d 。其他費用: 按實際發生計算。
效果確定:潰瘍癒合標準按胃鏡常規評定標準判定,HP 根除以兩項檢查均為陰性為判斷標準, 如潰瘍癒合、 HP根除則為有效,否則為無效。 A 組有效率為 87.5% ,B 組有效率為 92.2% 。
成本 - 效果比分析: 成本 - 效果比分析的目的在於通過分析尋找達到某一治療效果時成本最低的治療方案, 通常採用成本( C ) 與效果( E ) 比值法,其可將成本與效果兩者有機地聯繫在一起, 它是採用單位效果所花費的成本來表示的,一般比值越低, 該方案的實施就越有益。在對不同治療方案比較時,有的方案可能花費的費用成本很多,而且產生的效果也很好( 但有時也會出現相反的結果) , 而增加效果則需要增加病人的支出, 因此就要考慮每增加一個效果單位所花費的成本, 即增量成本 / 效果( △C/△E ) 比, 它代表一個方案成本 -效果與另一個方案比較而得到的結果, 以成本較低一組作為參照,另一方案與之對比而得到 △C/△E 。兩種根除 HP 治療方案的成本 - 效果分析見表。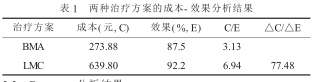

兩種治療方案的成本 - 效果比分析結果

