彈性力學的一個分支,又稱非線性彈性理論,是經典線性彈性力學的推廣。非線性彈性力學問題分為三類:物理線性、幾何非線性問題;物理非線性、幾何線性問題;物理非線性、幾何非線性問題。
基本介紹
- 中文名:非線性彈性力學
- 外文名:Nonlinear theory of elasticity
- 地位:經典線性彈性力學的推廣
- 又稱:非線性彈性理論
- 分類:物理線性、幾何非線性問題
- 拼音:feixianxing tanxinglixue
兩種非線性,物理非線性,幾何非線性,研究歷史,變形描述,幾何方程,本構方程,其它問題,
兩種非線性
非線性彈性力學中存在兩種非線性:物理非線性和幾何非線性。兩種非線性是彼此無關的。
物理非線性
物理非線性,即應力-應變關係中的非線性。橡皮、高分子聚合物和生物軟組織等材料的應力-應變關係中有這種非線性。
幾何非線性
幾何非線性,即應變-變形梯度關係中的非線性。在薄板、薄殼、細桿、薄壁桿件的大變形問題和穩定問題中存在幾何非線性。
研究歷史
早在1894年,J.芬格就提出超彈性體的有限變形理論。有限變形理論的方程冗長、複雜,並具有強烈的非線性,當時的人們感到在數學上進行一般性的討論沒有多大希望。所以這方面的研究工作長時間進展不大。
1940年M.穆尼通過大量實驗,提出某些類型的橡皮的彈性勢函式表達式,從而把非線性彈性理論中難題之一的彈性勢函式的形式問題向前推進了一步,並證實橡皮是幾乎不可壓縮的材料,使它有了進一步和發展。
1948年R.S.里夫林在任意形式的貯能函式下,得到不可壓縮彈性體的幾個簡單而重要問題的精確解。將它們套用於橡膠製品,即使橡膠的伸長為原長的兩三倍,精度仍能達到百分之幾。在這一成就的鼓舞下,學者們重新開始探討有限變形彈性理論,並導致了整個的蓬勃發展。此後,非線性彈性理論就成為理性力學的重要組成部分。1952年起C.特魯斯德爾、W.諾爾、B.D.科勒曼、J.L.埃里克森、M.E.格廷、A.C.愛林根以及美籍華人王釗誠在非線性彈性力學方面作出較大貢獻,中國的郭仲衡於1962~1963年連續發表了多篇論文。1972年奧登等人在用有限元法進行數值解方面做了大量有成效的工作,從而使得非線性彈性力學在工程實際中得到較廣泛的套用。但是非線性彈性力學無論在理論方面、精確解方面還是數值近似解方面都比線性彈性力學難度大,所以至今遠不如線性彈性力學成熟,有許多問題尚需進一步探討。非線性彈性力學的基本概念和方程比較複雜,在分析中大多採用張量這一數學工具。
變形描述
變形描述在討論非線性彈性力學問題時,取初始時刻物體在三維空間中所占的區域為參考構形(見),在其上取笛卡兒坐標。在時刻物體所占的區域為現時構形,在其上取笛卡兒坐標。
由方程
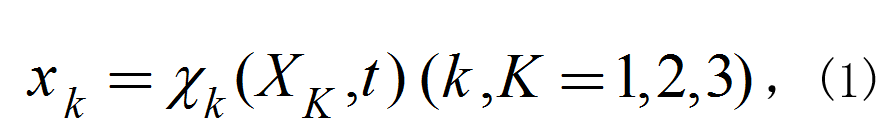
對於有單值逆變換的情形,存在

在時刻物質點的位置矢量為X,在運動過程中,該點在時刻的位置矢量為,則

在時刻物質點的位置矢量為X,在運動過程中,該點在時刻的位置矢量為,則
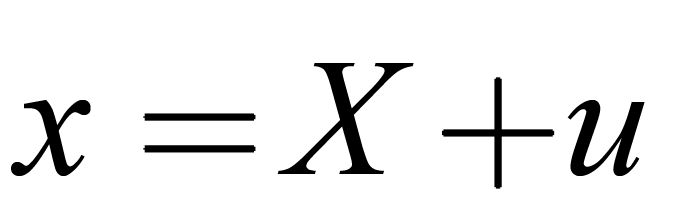
其中u是該物質點的位移矢量,它在 和
和 中的坐標分別記為
中的坐標分別記為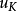 和
和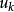 。
。


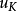
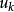
必須區分使用 和
和 坐標,這是非線性彈性力學區別於線性彈性力學的基本特徵之一。
坐標,這是非線性彈性力學區別於線性彈性力學的基本特徵之一。


描述物體變形的量有變形梯度,在 中,其定義為:
中,其定義為:


其中 為克羅內克符號;
為克羅內克符號; 為位移分量的偏導數,即變形梯度既包含純變形又包含剛性轉動,為把純變形從其中分解出來,須採用極分解定理,相應於左分解和右分解分別得到左柯西-格林應變
為位移分量的偏導數,即變形梯度既包含純變形又包含剛性轉動,為把純變形從其中分解出來,須採用極分解定理,相應於左分解和右分解分別得到左柯西-格林應變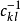 (又稱芬格應變)和右柯西-格林應變
(又稱芬格應變)和右柯西-格林應變 (又稱格林變)。而在
(又稱格林變)。而在 中有逆應變
中有逆應變 (稱為皮奧拉應變)和
(稱為皮奧拉應變)和 (稱為柯西應變)。為了使略去非線性項後所得應變與線性彈性力學中的應變相同,在坐標
(稱為柯西應變)。為了使略去非線性項後所得應變與線性彈性力學中的應變相同,在坐標 中還定義了拉格朗日應變
中還定義了拉格朗日應變 ,相應於坐標
,相應於坐標 則定義歐拉應變
則定義歐拉應變 ,這六種應變在理性力學中稱為變形張量。
,這六種應變在理性力學中稱為變形張量。


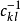








近代非線性彈性力學採用變形梯度作為最基本變行量,其他應變都可由它定義或導出。非線性彈性力學較常使用上述六種應變,而線性彈性力學只使用一種應變,即在 中略去位移偏導數的二次項(非線性項)後的應變。
中略去位移偏導數的二次項(非線性項)後的應變。

幾何方程

非線性彈性力學的幾何方程(6)和(7)是關於位移偏導數的非線性方程,所以是幾何非線性的。而方程(8)和(9)是線性彈性力學中的幾何方程。在非線性彈性力學中(6)和(7)是有區別的,而線上性彈性力學中(8)和(9)沒有區別。
非線性彈性力學中的物理意義、數學意義與線性彈性力學中的相同。但由於幾何方程比較複雜,故需要採用張量的方法,利用黎曼曲率張量在歐氏空間中為零的條件導出應變協調方程。
應力和平衡方程在變形後的構形上定義應力是最自然的,這種應力稱為柯西應力(或歐拉應力) 。但因變形後的構形是未知的(待求的),故取變形前的構形上單位面積的面力作為應力的定義,這種應力稱為皮奧拉應力(或拉格朗日應力、第一皮奧拉-基爾霍夫應力)
。但因變形後的構形是未知的(待求的),故取變形前的構形上單位面積的面力作為應力的定義,這種應力稱為皮奧拉應力(或拉格朗日應力、第一皮奧拉-基爾霍夫應力) 。由於
。由於 是非對稱的,故又定義對稱的應力
是非對稱的,故又定義對稱的應力 ,稱為基爾霍夫應力(或第二皮奧拉-基爾霍夫應力)。此外還有另一種對稱的應力
,稱為基爾霍夫應力(或第二皮奧拉-基爾霍夫應力)。此外還有另一種對稱的應力 槓,稱為對流應力。
槓,稱為對流應力。 是真實應力,
是真實應力, 、
、 和
和 槓是名義應力。非線性彈性力學中,有上述四種應力,而線性彈性力學中只有一種應力。線上性化的近似假設下,非線性彈性力學的四種應力都化為一種應力,即線件彈性力學中應力。
槓是名義應力。非線性彈性力學中,有上述四種應力,而線性彈性力學中只有一種應力。線上性化的近似假設下,非線性彈性力學的四種應力都化為一種應力,即線件彈性力學中應力。









由於有多種形式的應力。所以相應地有多種形式的動力學方程,它們都描述變形後物體構形中微體的動g量守恆條件和動量矩守恆條件。由於 、
、 、
、 槓和
槓和 中含有變形梯度,故在平衡微分方程中含有位移的偏導數,而線上性彈性力學中,平衡微分方程不含位移偏導數。由於平衡方程中應力與位移耦合,所以非線性彈性力學同線性彈性力學相比在數學處理上要繁難得多。
中含有變形梯度,故在平衡微分方程中含有位移的偏導數,而線上性彈性力學中,平衡微分方程不含位移偏導數。由於平衡方程中應力與位移耦合,所以非線性彈性力學同線性彈性力學相比在數學處理上要繁難得多。




本構方程
本構方程線上性彈性力學中,本構方程(即應力-應變關係)只有一種形式,即給出的方程,其圖像是一條直線。在非線性問題中,由於應力和應變都有多種形式,所以有多種本構方程,其圖像是曲線(非線性),但載入、卸載是同一條曲線(與塑性力學不同)。究竟哪種應力跟哪種應變對應,就要從基本的本構公理(見本構關係)出發來考慮。
非線性彈性力學主要通過以下兩個基本模型建立本構方程:①彈性體理想模型。該模型假設:存在各處應力為零的自然狀態,初始構形就取在自然狀態上,材料行為只與相對於自然狀態的現時變形狀態有關。可以通過兩種途徑來建立相應的本構方程。一種是格林方法,即從勢能函式出發來得到彈性體的本構方程。彈性勢是任何一個應變均可作為自變數的標量函式。具有彈性勢的彈性體稱為超彈性體或格林意義下的彈性體。另一種是柯西方法,從彈性體的特性即“一定的應力狀態對應於一定的應變狀態”出發,直接假設應力-應變函式關係,再通過實驗確定其中係數。直接由這種應力-應變函式關係描述的物體叫柯西意義下的彈性體,或直接叫作彈性體。各向同性超彈性體一定是各向同性彈性體,但彈性體只有當其應力- 應變關係中的係數滿足一定的關係時才是超彈性體,才具有相應的彈性勢。在這個意義上說來,柯西彈性體是一個比超彈性體更為廣泛的概念。②低彈性體模型。1955年特魯斯德爾從時間變化率出發,為體現簡單變率理論的理想模型而引出低彈性的概念。應力的本構導數是變形速率的線性齊次函式的物體叫作低彈性體。諾爾證明應力關係 =
= (
(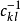 )可逆的各向同性彈性體是低彈性體。各向異性彈性體不是低彈性體。小應變低彈性體是彈性體。
)可逆的各向同性彈性體是低彈性體。各向異性彈性體不是低彈性體。小應變低彈性體是彈性體。


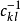
彈性體、超彈性體都假設存在一個自然狀態,而低彈性體完全不需要這個假設。低彈性理論和有限彈性應變經典理論體現不同的彈性概念,其中任何一個不能包括另一個。在幾何線性、物理線性和存在自然狀態的前提下,低彈性、彈性、超彈性三者等價。
其它問題
非線性彈性力學中的各變分原理都可從虛功原理統一導出,方法和步驟同線性彈性力學中的相同。非線性彈性力學的應力、應變形式多種多樣,對應的變分原理的形式也比線性彈性力學中多。在非線性彈性理論中,是否存線上性理論中那種應力場是唯一獨立變數的余能原理,是一個近年來引起廣泛興趣的問題。平衡方程中應力與位移的耦合,使這一問題至今尚未徹底解決,甚至問題的這種提法是否恰當也有待研究。
