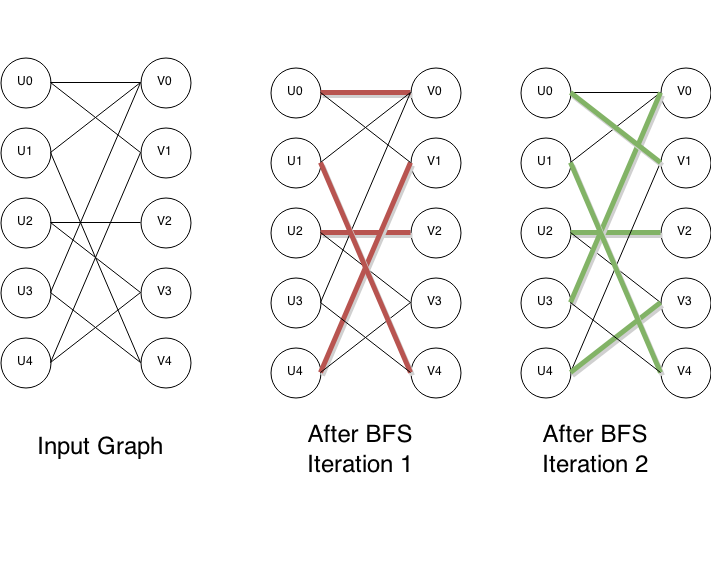
在計算機科學中，Hopcroft-Karp算法是一種算法，它將二分圖作為輸入，並產生最大基數匹配一組儘可能多的邊，其特性是沒有兩條邊共享一個端點。
該算法由John Hopcroft和Richard Karp（1973）發現。正如之前的匹配方法，如匈牙利算法和Edmonds（1965）的工作一樣，Hopcroft-Karp算法通過尋找增廣路徑反覆增加部分匹配的大小：在進入和離開之間交替的邊緣序列。
基本介紹
- 中文名：霍普克洛夫特－卡普算法
- 外文名：Hopcroft-Karp
- 提出者：John Hopcroft和Richard Karp
- 提出時間：1973年
增加路徑,算法,分析,
增加路徑
在某些部分匹配
中不是邊緣端點的頂點稱為自由頂點。算法所依賴的基本概念是增強路徑，從自由頂點開始，在自由頂點結束的路徑，以及在路徑中不匹配和匹配的邊之間交替的路徑。根據該定義，除了端點之外，擴充路徑中的所有其他頂點（如果有的話）必須是非自由頂點。增強路徑可以僅由兩個頂點（兩個都是自由的）和它們之間的單個不匹配邊緣組成。
如果 是匹配的，並且
是相對於 的擴充路徑，那么兩組邊的對稱差異，
將與大小
形成匹配因此，通過找到增強路徑，算法可以增加匹配的大小。
相反，假設匹配的 不是最優的，讓 為對稱差異
其中
是最佳匹配。因為 和 都是匹配，所以每個頂點在 中的度數最多為2。所以 必須形成一個集合不相交周期， 中具有相同數量的匹配和不匹配邊的路徑，增加 的路徑，以及增加 的路徑*;但後者是不可能的，因為 是最優的，具有相同數量的匹配和不匹配頂點的周期和路徑不會導致 和 之間的大小差異，因此這個差異等於 中 的擴充路徑的數量。因此，只要存在匹配的 大於當前匹配的 ，還必須存在增強路徑。如果沒有找到擴充路徑，則算法可以安全地終止，因為在這種情況下 必須是最優的。
匹配問題中的增強路徑與在最大流動問題中產生的增大路徑密切相關，沿著該路徑可以增加流動的端子之間的流動量。可以將二分匹配問題轉換為最大流動實例，使得匹配問題的交替路徑成為增加流動問題的路徑。實際上，將Hopcroft-Karp算法中使用的技術推廣到任意流網路被稱為Dinic算法。
算法
該算法可以用以下偽代碼表示。
輸入：二分圖
輸出：匹配
重複
until
更詳細地說，讓
和
為
的兩個分區中的兩個集合，並讓 與 匹配任何時候V都表示為集 .算法分階段運行。每個階段包括以下步驟。
廣度優先搜尋將圖的頂點劃分為多個層。 中的自由頂點用作此搜尋的起始頂點，並形成分區的第一層。在搜尋的第一級，只有不匹配的邊，因為 中的自由頂點根據定義不與任何匹配的邊相鄰。在隨後的搜尋級別，遍歷的邊緣需要在匹配和不匹配之間交替。也就是說，當從 中的頂點搜尋後繼者時，可以僅遍歷不匹配的邊，而從 中的頂點可以僅遍歷匹配的邊。搜尋終止於第一層
，其中到達 中的一個或多個自由頂點。
該算法找到長度為 的最大頂點不相交增廣路徑集。 （最大意味著不能再添加這樣的路徑。這與找到這樣的路徑的最大數量是不同的，這將更難做到。幸運的是，這裡找到最大路徑集就足夠了。）這個集合可能是通過深度優先搜尋（DFS）從 到 中的自由頂點計算，使用廣度第一層來指導搜尋：DFS只允許跟隨導致未使用的邊緣上一層中的頂點，DFS樹中的路徑必須在匹配和不匹配的邊之間交替。一旦找到涉及 中的一個頂點的擴充路徑，DFS將從下一個起始頂點繼續。在DFS期間遇到的任何頂點都可以立即標記為已使用，因為如果在DFS的當前點沒有從它到 的路徑，那么該頂點不能用於到達 在DFS的任何其他地方。這確保了DFS的
運行時間。也可以在另一個方向上工作，從 中的自由頂點到 中的自由頂點，這是偽代碼中使用的變體。
以這種方式找到的每條路徑都用於放大 .
當在其中一個階段的廣度優先搜尋部分中找不到更多增強路徑時，該算法終止。
分析
每個階段包括單個廣度優先搜尋和單個深度優先搜尋。因此，可以在 時間內實現單個階段。因此，在
的圖形中，第一個階段頂點和邊緣，花費時間
。
可以示出每個階段將最短增強路徑的長度增加至少一個：該階段找到給定長度的最大增強路徑集合，因此任何剩餘的增強路徑必須更長。因此，一旦算法的初始階段完成，最短的剩餘擴充路徑至少具有邊緣。然而，最終相位和由初始相位找到的部分匹配M的對稱差異形成頂點不相交的增廣路徑和交替循環的集合。如果此集合中的每個路徑的長度至少為，則最多可以集合中的路徑，最佳匹配的大小最多不同於的大小邊緣。由於算法的每個階段都將匹配的大小增加了至少一個，因此在算法終止之前，最多可以有個附加階段。
由於該算法最多執行
階段，因此總時間為）在最壞的情況下。
然而，在許多情況下，算法所花費的時間甚至可能比這種最壞情況分析所指示的更快。例如，在稀疏二分隨機圖的平均情況下，Bast等。 （2006）（改進了Motwani 1994的先前結果）表明，所有非最優匹配都具有高機率增強的對數長度路徑。因此，對於這些圖，Hopcroft-Karp算法採用
階段和
總時間。
