電磁波干涉是指兩列或兩列以上的電磁波在空間中重疊時發生疊加,從而形成新波形的現象。
基本介紹
- 中文名:電磁波干涉
- 外文名:Electromagnetic wave interference
- 學科:物理學
- 定義:電磁波在空間中重疊時發生疊加
- 套用:電磁干擾
- 種類:相長干涉、相消干涉
干涉條件
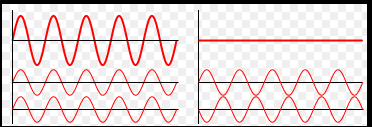
理論基礎
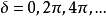
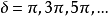
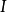
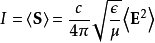
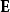
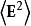

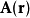
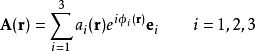
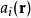
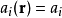
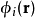
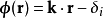
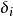
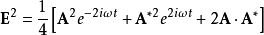
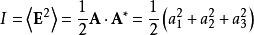
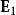

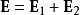
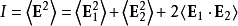
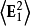
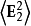
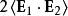
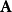
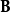
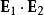
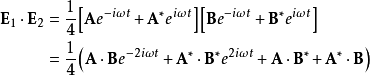
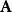
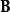
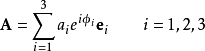


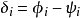
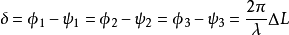
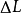
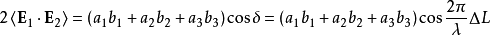

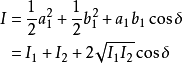

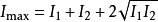
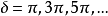
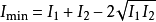
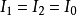

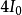
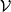
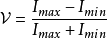
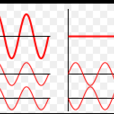
電磁波干涉是指兩列或兩列以上的電磁波在空間中重疊時發生疊加,從而形成新波形的現象。

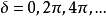
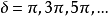
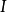
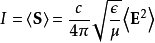
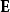
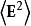

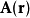
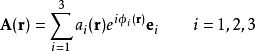
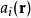
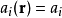
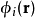
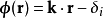
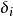
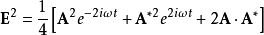
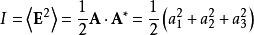
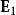

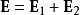
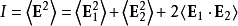
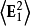
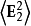
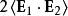
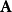
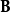
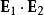
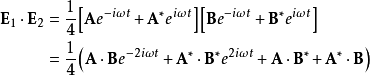
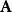
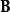
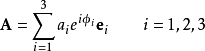


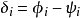
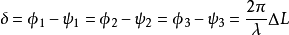
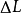
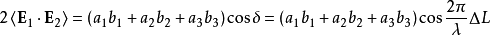

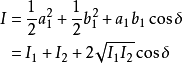

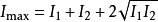
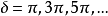
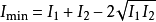
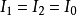

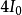
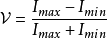
電磁波干涉是指兩列或兩列以上的電磁波在空間中重疊時發生疊加,從而形成新波形的現象。...
物理學中,干涉(interference)是兩列或兩列以上的波在空間中重疊時發生疊加從而形成新的波形的現象。例如採用分束器將一束單色光束分成兩束後,再讓它們在空間中的...
干涉現象是指同振幅、頻率和初位相的兩列(或多列)波的疊加合成而引起振動強度重新分布的現象。在波的疊加區有的地方振幅增加,有的地方振幅減小,振動強度在空間...
電磁波衍射指電磁波遇到障礙物時偏離原來直線傳播的物理現象。任何波都具有衍射的固有性質。然而,不同情況中波發生衍射的程度有所不同。如果障礙物具有多個密集分布...
電磁波,是由同相且互相垂直的電場與磁場在空間中衍生髮射的震盪粒子波,是以波動的形式傳播的電磁場,具有波粒二象性。電磁波是由同相振盪且互相垂直的電場與磁場...
干涉型吸波材料是指材料表面的反射波與進入材料由反射背襯(通常為金屬板)返回的出射波發生相干,從而使反射減小或消失的一類材料。...
無線電頻率干涉是指隨著工業與科技的飛速發展,微波波段被趙來越多地運用於軍、民用的通訊系統中,星載微波福射計接收到的來自自然地氣系統的被動熱福射信號與通訊...
《光與電磁波》是2003年科學出版社出版的圖書,作者是熊纓。本書既可作為電子、通信、遙感、機械等相關專業本科生及非相關專業研究生的教材,又可供相關專業領域的...
干涉測量術(英語:Interferometry)是通過由波的疊加(通常為電磁波)引起的干涉現象來獲取信息的技術。這項技術對於天文學、測速以及驗光等領域的研究都非常重要。...
其內部覆蓋有電磁波吸波材料,不同之處在於半電波暗室使用導電地板,不覆蓋吸波...直射波受從周圍物體反射的干涉,在測試區域形成場的變化,由於該波波程差作為位置...
圖書信息電磁波禁止及吸波材料(第二版) 所屬類別 科技 >> 材料 >> 材料綜合 作者:劉順華、劉軍民、董星龍、段玉平 等編著 出版日期:2014年1月 書號:978-7-...
干涉儀是很廣泛的一類實驗技術的總稱, 其思想在於利用波的疊加性來獲取波的相位信息, 從而獲得實驗所關心的物理量。干涉儀並不僅僅局限於光干涉儀。 干涉儀在天文...
地震波干涉法(Seismic Interferometry)是最近幾年地球物理特別是勘探地球物理研究的一個熱點。地震波干涉法與物理學中的干涉法類似,但研究對象為地震信號或聲信號,其...
在空間傳播著的交變電磁場,即電磁波。它在真空中的傳播速度約為每秒30萬公里。電磁波包括的範圍很廣。實驗證明,無線電波、紅外線、可見光、紫外線、X射線、γ...
亦稱“微波吸收材料”。能將入射的電磁波能量轉換為其他形式的能量而極少被反射回去的材料。按吸收機理,分為吸收型、干涉型、諧振型和電漿型電磁波吸收材料。按...
電磁波在傳播過程中,由於傳播媒介及傳播途徑隨時間的變化而引起的接收信號強弱變化的現象叫作衰落。譬如在收話時,聲音一會兒強,一會兒弱,這就是衰落現象。...
震波干涉法(Seismic Interferometry)與物理學中的干涉法類似,但研究對象為地震信號或聲信號,其廣義的定義是指與地震波有關的干涉現象的研究。通過對記錄到的地震...
多徑效應(multipath effect):指電磁波經不同路徑傳播後,各分量場到達接收端時間不同,按各自相位相互疊加而造成干擾,使得原來的信號失真,或者產生錯誤。比如電磁波沿...
