基本介紹
- 中文名:電子對電磁波散射和吸收的經典理論
基本信息,經典理論,
基本信息
當外來電磁波入射到電子(自由電子或束縛的諧振電子)上時,電子就會在外來電磁波的作用下作受迫振動。由於作這種振動,電子將不斷地向外輻射電磁波。通常把這種輻射波稱為次波,而把入射電磁波稱為原波。次波是向各個方向放射的,它的能量又來源於原波,故上述過程總的結果可歸結為入射來的電磁波被電子散射到各個方向去。因而這個過程被稱為電子對電磁波的散射。處於諧振電子的情況,當外來電磁波的頻率與諧振電子的固有頻率相同時,過程又顯示新的特點,這時電子由於共振而強烈地吸收原波的能量,它的數值常比一般散射的能量大好多個量級。吸收的能量一部分常通過某種途徑(例如振子間的碰撞)轉化為熱能,一部分被振子輻射出去。後者稱為吸收-再放射,或稱共振散射。
經典理論
自由電子的散射 這裡只考慮電子在外來電磁波作用下作受迫振動而且其速度始終比真空中光速 с小得多的非相對論情況(這要求峛《с,為電,子電荷,為電子靜質量,為入射波電場振幅,峛為入射波的約化波長,即波長被2除)。當《с時,電子受入射波中磁場的作用力可以略去,於是電子將不漂移而在一固定點附近振動,在這種情況下,散射波的頻率將與散射方向無關,並等於入射波的頻度。《с還保證了電子的振幅比入射波波長小得多,從而散射波可通過電偶極輻射公式來計算。在入射波非偏振的情況下,空間任一點P的散射波的強度(能量流密度的周期平均值)為
波散射和吸收的經典理論 title=電子對電磁波散射和吸收的經典理論>,
<img style="float: right;" title="電子對電磁式中代表入射波的強度,代表散射角即與入射方向間的夾角(O為振動中心),即為從振動中心O到P的距離。為電子的經典半徑(見電磁質量和輻射阻尼),其值等於(本條採用高斯制單位)。
電子對電磁波散射和吸收的經典理論
上式表明,散射強度與入射波的頻率無關,它隨角度的分布由因子(1+cos)表示,對於向前和向後散射是對稱的。將各方向的散射能量總加起來,就得出電子單位時間內向各個方向散射的總能量為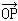 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論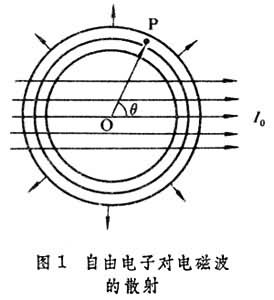 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
上式表明,散射強度與入射波的頻率無關,它隨角度的分布由因子(1+cos)表示,對於向前和向後散射是對稱的。將各方向的散射能量總加起來,就得出電子單位時間內向各個方向散射的總能量為
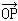 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
它等於入射波中這樣一塊橫截面上的能量流。因此,這個截面被稱為散射截面。上面討論的非相對論自由電子的散射截面即為 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論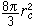 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論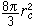 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
它的數值很小,等於以電子經典半徑。所作的圓面積的倍,自由電子就是把入射波中相當於這樣大一塊橫截面中流來的能量散射到其他方向去。
以上結果通常稱為湯姆孫散射公式,稱為湯姆孫截面。在量子電動力學理論中,當光子的能量比電子靜能量小得多時(即),也得到與此相同的結果。
對於電子來說,湯姆孫公式直到軟X 射線都能適用。例如對於波長為2.4埃的X 射線,,比1還小得多。
關於硬X 射線和γ射線與自由電子的散射,量子效應已經顯著。它具有新的特點,通常稱為康普頓散射(見康普頓效應)。
諧振電子的散射 對於諧振電子,當入射波為非偏振的平面波時,散射強度為 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論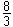 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論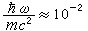 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
以上結果通常稱為湯姆孫散射公式,稱為湯姆孫截面。在量子電動力學理論中,當光子的能量比電子靜能量小得多時(即),也得到與此相同的結果。
對於電子來說,湯姆孫公式直到軟X 射線都能適用。例如對於波長為2.4埃的X 射線,,比1還小得多。
關於硬X 射線和γ射線與自由電子的散射,量子效應已經顯著。它具有新的特點,通常稱為康普頓散射(見康普頓效應)。
諧振電子的散射 對於諧振電子,當入射波為非偏振的平面波時,散射強度為
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論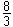 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論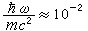 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
角分布與自由電子散射一樣,但隨著頻率而變化。式中為振子的固有頻率,標誌輻射阻尼作用。γ的值一般比小得多(見電磁質量和輻射阻尼)。相應的散射截面為 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論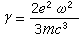 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論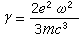 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
為前述湯姆孫截面。當時
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論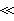 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
即散射截面與頻率的四次方成正比。這個關係通常稱為瑞利散射定律。在的情況,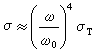 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
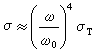 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論σ≈σT,
即化為自由電子的結果。這表明,對於高頻電磁波,束縛力可忽略,諧振電子的散射行為變得與自由電子相同。
對於上述兩種情況,散射截面都很小,具有娪或更小的量級。但是當=時,截面變成了一個很大的值
對於上述兩種情況,散射截面都很小,具有娪或更小的量級。但是當=時,截面變成了一個很大的值
,
其中代表頻率為的電磁波的約化波長。即截面從娪 的量級猛增到峛娿的量級。對可見光來說, 約增大了10倍。數量上如此巨大的差異,表明事物的性質已發生了變化。
在以上()的公式中,只考慮了輻射阻尼而沒有考慮其他的阻尼效應。考慮其他阻尼時,應分別計算散射截面和總吸收截面(見下文)。
諧振子的吸收 進一步討論在附近時過程的特點。假設除輻射阻尼以外,還有其他形式的阻尼(如碰撞阻尼)。振子單位時間內從入射波吸收的能量,可根據入射波的電場對振子作的功來計算,其值為 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
在以上()的公式中,只考慮了輻射阻尼而沒有考慮其他的阻尼效應。考慮其他阻尼時,應分別計算散射截面和總吸收截面(見下文)。
諧振子的吸收 進一步討論在附近時過程的特點。假設除輻射阻尼以外,還有其他形式的阻尼(如碰撞阻尼)。振子單位時間內從入射波吸收的能量,可根據入射波的電場對振子作的功來計算,其值為
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
其中代表總的阻尼效應,=+′,仍為輻射阻尼的貢獻,在這裡可取作,′則代表其他形式的阻尼效應。振子吸收來的能量一部分再輻射出去,一部分通過其他形式的阻尼轉化為熱能。
定義總吸收截面,使就等於入射波中通過這樣大一塊橫截面流來的能量。按照此定義 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
定義總吸收截面,使就等於入射波中通過這樣大一塊橫截面流來的能量。按照此定義
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論。
σa在ω=ωo
σa在ω=ωo
附近顯示下列特點:
① 吸收截面在=處呈現為一尖銳高峰,其寬度為。
② 當阻尼增大因而的值增大時,寬度增加,但峰值()降低,峰的總面積不變,其值為
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論。
這一結果意味著,當入射波是具有連續譜的波時,振子在=附近單位時間吸收的總能量將與阻尼的大小無關,其值為 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
()代表入射波的強度密度在振子頻率處的值。
電子對電磁波散射和吸收的經典理論
振子散射出來的能量與總吸收能量的比等於輻射阻尼貢獻的與總的比。於是振子單位時間內散射的能量為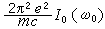 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
振子散射出來的能量與總吸收能量的比等於輻射阻尼貢獻的與總的比。於是振子單位時間內散射的能量為
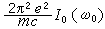 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論。
以上討論表明,振子在譜線附近從連續譜入射波中吸收的能量總是一定的,不受阻尼情況的影響,因此這種過程稱為本徵吸收。阻尼的影響只在於吸收能量的消耗分配上。標誌其他阻尼效應的′愈小,散射出去能量所占的比例就愈大。若′等於零,全部吸收來的能量都將用於散射。
在量子電動力學的理論中,求出的諧振子單位時間從連續譜入射波吸收的總能量同樣是 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
在量子電動力學的理論中,求出的諧振子單位時間從連續譜入射波吸收的總能量同樣是
 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論,
與上述經典理論所給的值相同。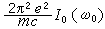 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論
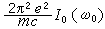 電子對電磁波散射和吸收的經典理論
電子對電磁波散射和吸收的經典理論