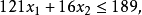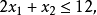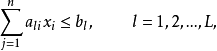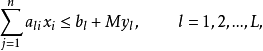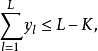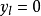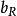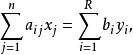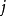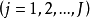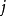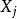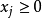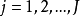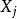離散最佳化

離散最佳化問題，又稱為整數規劃 (線性整數規劃)，整數規劃是指規劃中的變數（全部或部分）限制為整數，若線上性模型中，變數限制為整數，則稱為整數線性規劃。目前所流行的求解整數規劃的方法往往只適用於整數線性規劃，這是一類要求問題的解中的全部或一部分變數為整數的數學規劃。從約束條件的構成又可細分為線性，二次和非線性的整數規劃。

基本介紹

• 中文名：離散最佳化問題
• 外文名：discrete optimizing
• 所屬學科：數學
• 別名：整數規劃、線性整數規劃
• 分類：純整數、混合整數、0-1規劃等

基本介紹

離散最佳化問題，又稱為整數規劃 (線性整數規劃)，它是一定全部決策變數取整數值，就稱它為 “純整數規劃”；若允許一部分決策變數是連續的， 又限制其餘決策變數取整數值，則稱它為“混合整數規劃”；限制全部決策變數不是0就是1，就稱它為 “二進制規劃”或“0-1”規劃。後者是一類特殊的離散最佳化問題。

相關準則

已經發展了很多種建立整數規劃的準則，人們運用它取得一些很有用的模型，這通常是指在一個計算機上，模型的求解會在比較短的時間內完成。 下面列舉出某些準則。

①如果事先知道一個整數變數會是一個大的數值(通常為20，或者更大)，就把它作為連續變數處理，然後對該變數的解，按照四捨五入原則取整而得到整數解答。

②約束條件係數太繁瑣會使求解困難，所以要慎重地把約束條件寫成儘可能不複雜的形式。例如，設為非負整數變數，約束條件為

可以換成如下的等價表達式

③由於可行域範圍的任何縮小都會減小計算工作量，所以希望對變數取一個較好的上界和下界。

在實踐中，為了解決某些問題建立模型的困難，也會引進離散模型。如以下情況：

①研究兩個約束條件中至少有一個成立的情況。例如，製造某一產品，我們要從兩種資源中選取出一種。這種情況顯然包括“兩取一”約束條件在內。例如，我們會遇到下列約束條件：

或

或

設M為非常大的正數，又定義y為雙值變數(取值 為0或1)，則“兩取一”約束條件的等價表達式為

注意在最後的解答中，若y=0，則第一個約束條件成立，第二個約束條件就變得不起作用(因為賦予M非常大的數值)。若y=1，則情況相反。

②推廣前面的方法，即研究L個約束條件中至 少有K (K<L)個成立的情況。設L個約束條件為

其中至少有K (K<L)個成立。這種約束條件的等價表達式為

式中，M是一個非常大的正數，或1，。

③有時會碰到下面這種情況，即某一函式只能取R個特定值中的一個。如果把這個限制寫成為

或或或.

那么等價的表達式為

式中，或1，。

還值得指出的是，變數有界(明顯或者隱含)的純整數規劃問題，可以用一種稱為“二進制分解”方法將其轉變為0-1規劃，另外，這方法也可把非線性多項式0-1規劃轉變為線性0-1規劃。

例題解析

例1設背包的有限容積為V，現有種物品可以往裡面裝，第種物品的每件體積為，價值為。裝背包的目標，是在背包容積的限制下，怎樣的裝法可使裝進背包的物品總價值最大。如果我們定義為裝進背包的第種物品的件數，則這個問題可以寫成

約束：

並是整數.

這個模型是推廣了的背包問題，其中可以取任意非負整數。換言之，裝進背包的某一種物品可以多於1件。背包問題的特殊情況之一，是限制每一個變數取值為0或1，因此裝進背包中的每種物品不能多於一件。

背包問題是只有一個約束條件的純整數規劃。 有兩點理由說明這種問題是很重要的。第一，很多整數規劃問題，諸如資金預算、工具機負荷和方案選擇等問題，都可以指出它的背包問題等價形式。第二，已經有很多求解背包問題的有效算法，它們已成為求解一般整數規劃問題新算法的基礎。

已經發展的離散最佳化問題的算法，典型地分為3類： 枚舉法，割平面法和群論法。