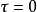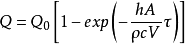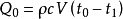集總參數法

當物體內溫差相差不大，可近似認為在這種非穩態導熱過程中物體內的溫度分布與坐標無關，僅隨時間變化。因此物體溫度可用其任一點的溫度表示，而將該物體的質量和熱容量等視為集中在這一點，這種方法稱為集總參數法。

基本介紹

• 中文名：集總參數法
• 外文名：Lumped parameter method
• 條件：物體的導熱係數要相當大
• 特點：這是一種理想化模型
• 別稱：集中參數法

使用條件

當物體的熱導率λ_s很大，表面積很大，表面傳熱係數h較小且厚度δ不大時，物體的內部導熱熱阻與表面傳熱熱阻相比可以忽略。此時物體中的溫差不大，溫度降落主要在物體表面。

由上述物理量可以組成畢渥數：Bi=hl_e/λ=內部導熱熱阻/外部傳熱熱阻

式中l_e為引用尺寸。對於無限大平壁l_e=δ/2；對於無線長圓柱體和球l_e=d/2=R（半徑）。

當Bi<<1時，物體符合用集總參數法簡化計算的條件。理論上可以證明，當Bi<0.1時，用集總參數法分析非穩態導熱問題誤差不超過5%。

導熱微分方程

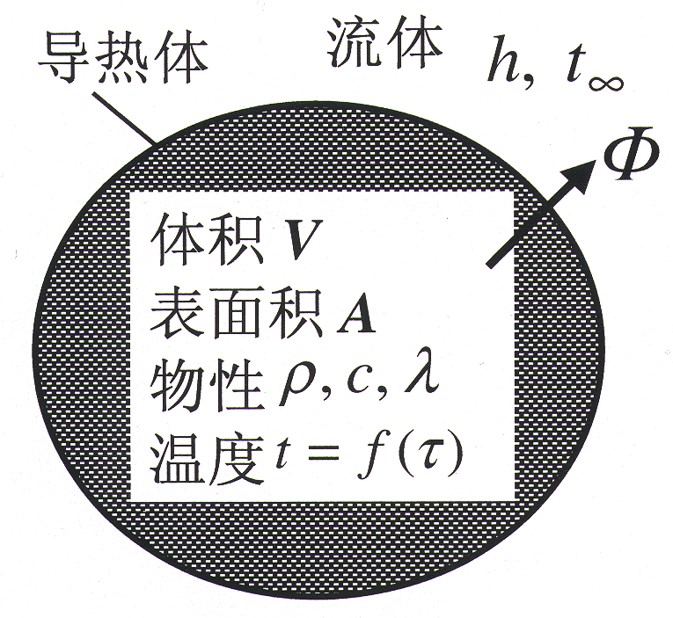
當溫度恆定時，設有一體積為V、傳熱表面面積為A、初始溫度為t₀、常物性無內熱源的任意形狀的固體，突然置於溫度為t₁（恆定）的環境中加熱或冷卻，物體表面與周圍環境的表面傳熱係數為h₀。假定此物體的內部導熱熱阻可以忽略，符合集總參數法簡化分析的條件。用導熱微分方程和定解條件求解。

由於物體內部的溫度與坐標無關，可得下式

Φ'/ρc

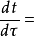
表面傳入的熱流量為：

Φ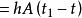

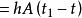
內熱源強度為：

Φ'=Φ/V=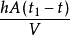

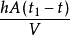
將上述公式整理，可得物體非穩態導熱的導熱微分方程：

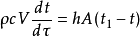
這就是符合集總參數法簡化分析的物體非穩態導熱的導熱微分方程。

傅立葉數

引入過餘溫度：

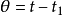
導熱微分方程變成齊次方程：

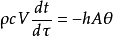
初始條件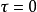時：

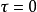
對導熱微分方程分離變數並積分可得：

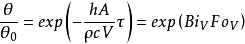
式中Fo便為傅立葉數。傅立葉數為無量綱常量。腳標“V”表示特徵尺寸l_c，具有長度的量綱。大平璧的特徵尺寸為δ/2；對於無線長圓柱體為R/2；球為3/R。

所以，集總參數法的判別式可變為：

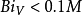
其中M為特徵尺寸與引用尺寸的比值。對於無限長大平璧M=1；對於無線長圓柱體和正方形柱體M=1/2；對於球和正方體M=1/3。

時間常數

由於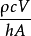有時間的量綱，所以稱為時間常數，記為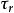。所以公式可變為：

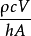
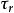
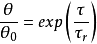
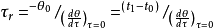
由此可見，時間常數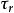表明內部熱阻可以忽略的物體突然被加熱或冷卻時，它以初始溫度變化速度從初始溫度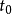變化到周圍流體溫度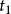所需要的時間。

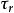
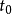
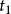
時間常數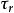是一個綜合量，既反映物體熱容量的大小，又反映表面傳熱情況。顯然，時間常數小，表明物體表面傳熱好，且本身熱容量也小，因為溫度變化快。但對於恆定的流體溫度，如時間足夠長，則時間常數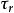的大小對測溫準確性沒有影響。

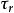
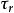
熱量

如果要計算從初始時刻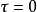到時刻通過物體傳熱表面傳遞的熱量Q，根據Q的定義代入式，可得：

式中，稱為物體的初始過余熱焓，單位為J，它表示物體由初始溫度變化為環境溫度時所吸收或放出的熱量。