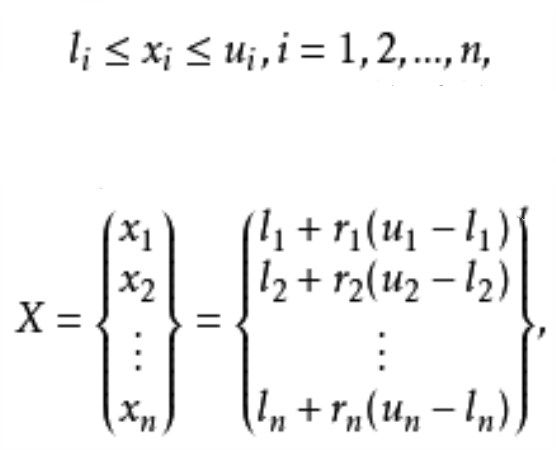隨機跳躍法

隨機跳躍法(random jump method)是利用隨機數尋求最優點的一種搜尋方法。設要求f(x)的極小點，x=(x₁，x₂，…，x_n)∈R，l_i≤x_i≤u_i(i=1，2，…，n)，式中l_i和u_i為變數x_i(i=1，2，…，n)的上限和下限.再設n個隨機數r₁，r₂，…，r_n在0和1之間均勻分布，套用每組隨機數求x：x=(x₁，x₂，…，x_n)=(l₁+r₁(u₁-l₁)，l₂+r₂(u₂-l₂)，…，l_n+r_n(u_n-l_n))，並計算f(x)，取使f(x)最小的x，它就作為所求的極小點。

基本介紹

• 中文名：隨機跳躍法
• 外文名：random jump method
• 所屬學科：數學
• 簡介：利用隨機數尋求最優點的搜尋方法

基本介紹

隨機搜尋法是基於用隨機數去尋找極小點。由於大多數計算機的程式庫都具有隨機數發生子程式，所以使用隨機搜尋法是很方便的，隨機跳躍法是隨機搜尋法的一種。

求解的問題為在n維超立方體內n維函式的極小，超立方體的定義為

式中，分別為變數的下界和上界。在隨機跳躍法中，要產生多組n個隨機數，這些隨機數均勻分布在0和1之間。而每一組隨機數都可被用來構造由式(1)所定義的超立方體內的一個點X，即

並可求出X點的函式值。通過生成大量的點和計算相應點的目標函式值，最後可取其中使為最小的點作為所要求的極小點。

例題解析

【例1】用隨機跳躍法求

的極小值。假定的範圍為。

解 產生的隨機數和所對應的設計變數值及目標函式值由表1所給出(為節省篇幅，表中僅列舉了使目標函式值有改善的數據)。表中可以看出已搜尋了10000次。

雖然隨機跳躍法很簡單，但對變數很多的問題不實用，僅適用於效率不重要的場合。

表 1

試驗序號	隨機數		對應的設計變數
	（1）	（2）	x1	x2
1	0.12606	0.63946	-7.47887	2.78913	67.65904
3	0.42469	0.84082	-1.50612	6.81649	22.14585
13	0.33082	0.86722	-3.38357	7.34448	16.40928
21	0.29605	0.69995	-4.07908	3.99909	8.56712
23	0.47964	0.51831	-0.40723	0.36612	-0.60582
118	0.42872	0.60919	-1.42552	2.18379	-1.00223
1238	0.43523	0.57343	-1.29534	1.46852	-1.05596
1836	0.43380	0.59430	-1.32398	1.88601	-1.14119
2451	0.44137	0.58901	-1.17266	1.78015	-1.20863
8573	0.44690	0.57240	-1.06193	1.44792	-1.23317
10000	無改進
正確解	——	——	-1.00000	1.50000	-1.25000