加密系統的安全性取決於秘密保護的數據，這些數據應該對已授權者可知，但是對其他人不可知且不可預測。實現不可預測特徵的方法就是部署隨機化。現代加密協定通常需要頻繁生成隨機的數量，在這個過程中破壞或利用弱點的攻擊被稱為隨機數生成器攻擊。
對於安全需求來說，高質量的隨機數發生（RNG）的過程幾乎總是有需要的。生成過程缺乏質量通常會導致受攻擊時的脆弱性，因此導緻密碼系統缺乏安全性，甚至完全不安全。RNG的過程對於攻擊者而言是特別有吸引力的，因為它通常位於一個孤立的易於定位的硬體或軟體。 如果攻擊者可以用一種他可以預測的偽隨機數替換RNG過程，安全性就會受到完全損害，但是上游的測試對此通常是無法偵測到的。不僅如此，這種攻擊只需要接入一次受攻擊的系統，不需要向攻擊者返回任何數據，換句話說，就是一個計算機病毒 ，偷取了密鑰然後用電子郵件向一些接受點傳送。
基本介紹
- 中文名：隨機數生成器攻擊
- 外文名：Random number generator attack
人工生成,攻擊,防禦,突出例子,
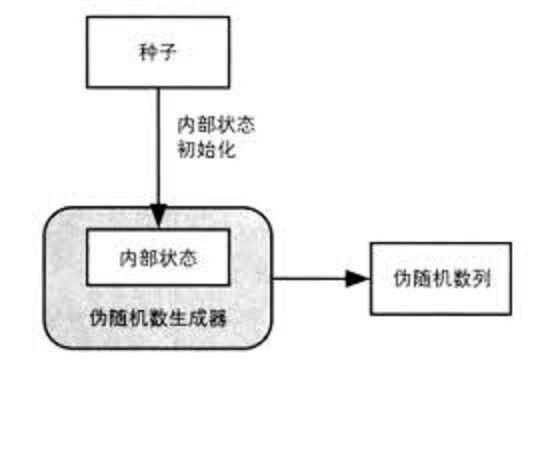
人工生成
人工生成的隨機數通常極差。魔術師，職業賭徒和騙子，他們都依賴於預測人的行為。 在第二次世界大戰中，德國代碼文員被指示隨機挑選三個字母作為恩尼格瑪密碼機中每條訊息的轉子初始設定。但是，有些人選取了可預測的值，比如他們的女友的姓名的首字母，這大大幫助了盟軍破譯德國的加密系統。另一個例子就是計算用戶選擇密碼的方式通常可以預測（參見密碼破解）。
攻擊
軟體隨機數生成器
僅作為加密系統的其它組件而言，軟體隨機數發生器在設計上應該能抵抗一定的攻擊。攻擊類型可能包括：
- 直接密碼分析攻擊
- 若攻擊者可以獲得隨機數生成序列的一部分，並且可以據此將發生器的輸出從真正的隨機流中區分出來時，此類攻擊可行。
- 以輸入為基礎的攻擊
- 修改發生器的輸入來進行攻擊，例如通過將現存的熵“清洗”出現有的系統，並把系統設定為已知的狀態。
- 狀態妥協擴展攻擊
- 在內部保密狀態的發生器在某個時間是已知的，據此可以預測未來發生器的輸出或恢復之前的輸出。 這可能發生在發生器剛剛啟動並且發生器僅擁有少量或沒有擁有任何熵的時候（特別是計算機剛剛啟動並且正在執行一個非常標準的操作序列的時候），因此在這個狀態下，攻擊者可能能夠獲得初步的猜測值。
硬體隨機數生成器
許多針對硬體隨機數生成器的攻擊都是有可能的，包括嘗試捕獲計算機的射頻發射（例如從電機噪音中推斷硬碟中斷時間），或者嘗試將受控的信號反饋到假定的隨機源當中（比如關閉熔岩燈中的燈光或是將已知的強信號反饋到音效卡）。
隨機數生成器顛覆
顛覆隨機數可以在密碼學安全偽隨機數生成器中使用隨機數種子值來生成，種子值雖然隱藏在軟體中，但是對攻擊者已知。相對較短，比如24到40比特，的種子可以是真正隨機的，可以防止重複，但是並不足以防止攻擊者恢復“隨機”生成的密鑰。
隨機數在使用前會通過數層特定的軟體和硬體。數據可能在外圍設備中生成，通過電纜傳輸，由作業系統組件收集並由系統調用進行檢索。這一過程中的任何一點都可以替換顛覆的數據，並且幾乎無法檢測。
僅僅需要數平方毫米就可以使用積體電路建造一個用於生成顛覆隨機數的硬體電路。通過將這種晶片放置在上游任何隨機性來源數位化的地方，就可以破壞最先進的硬體隨機數生成器，例如在輸出驅動晶片中甚至在把計算機與生成器連線起來的電纜中。破壞晶片可以帶有一個時鐘來來把操作啟動時間限制到單位初次啟動之後，並且還能通過接受測試，也可以帶有用於開關控制的無線電接收器。破壞晶片的安裝可以是國家情報服務機構對製造商的要求，或者是之後任何有物理訪問權的人。用於替換內置硬體隨機數生成器的CPU晶片的可以是任意的兼容晶片，其固件中可以包含已顛覆的隨機數生成器。
防禦
- 使用真正隨機的來源生成密碼。有些系統會代為用戶選擇隨機密碼而不讓用戶自行提交。
- 使用加密系統來記錄隨機數生成過程，並提供審計生成過程的方法。
- 在購買後保持對硬體的完全物理控制。
設計一個安全隨機數生成器至少要求與設計密碼系統的其它部分一樣高的水平。
突出例子
可預測的網景隨機數種子
在早期版本的網景傳輸層安全性協定（SSL）中的加密協定中使用了偽隨機數，來源是偽隨機數生成器根據三個變數派生的：一天中的時間、進程ID與父進程ID。這些偽隨機數相對而言通常是可預測的，因此熵值很低並且也少於隨機數，亦因此發現這一版本的SSL並不安全。Phillip Hallam-Baker於1994年向網景公司報告了問題所在，隨後也向CERN網路團隊的一位研究員報告。但是問題在發布前並未修復。1995年，Ian Goldberg與David Wagner發現了這一問題，二人當時因為網景公司拒絕透露其隨機數字生成器（靜默安全性）的細節，而不得不對目標代碼進行逆向工程。隨機數生成器在後來的版本（第二版及更高）中通過更強的隨機數種子（即從攻擊者的角度來看，更隨機和更高的熵）得到修復。
微軟使用未發布的算法來為其Windows作業系統生成隨機數值，並通過CryptGenRandom實用工具提供給用戶。2007年11月，來自耶路撒冷希伯來大學與海法大學的Leo Dorrendorf et al. 發布了一篇名為Cryptanalysis of the Random Number Generator of the Windows Operating System （Windows作業系統中的隨機數生成器的密碼學分析）的論文。文中指出了當時微軟的生成方法中的嚴重缺陷，結論基於對Windows 2000中代碼的反彙編，但是根據微軟的說法，這些代碼也存在於Windows XP。微軟已經表示，文中描述的問題已經在Windows的後續版本中得到解決，後者使用了不同的隨機數生成實現。
橢圓曲線DRBG中可能的後門
美國國家標準技術研究所（NIST）發布了“確定性隨機位發生器”，並且推薦於NIST的特刊800至890期中。其中叫Dual_EC_DRBG的生成器受到了國家安全局（NSA）的歡迎。Dual_EC_DRBG使用橢圓曲線加密並包含一組推薦使用的常量。2007年八月，來自微軟的Dan Shumow與Niels Ferguson顯示這些常量可以通過在算法中創建一個竊密學後門的方式來構建。2013年九月，The New York Times（紐約時報）發文稱“NSA向NIST於2006年接納的一向標準中植入了後門...名為Dual EC DRBG標準”，從而揭示了NSA對美國人民進行了惡意軟體攻擊。2013年12月，據路透社報導，愛德華·斯諾登（Edward Snowden）發布的檔案顯示，NSA已經向RSA安全局支付了1000萬美元，將Dual_EC_DRBG作為後者的默認加密軟體，也因此出現更多關於該算法包含NSA後門的擔憂。出於這些擔憂，2014年，NIST從其關於隨機數發生器的指導草案中撤銷了，推薦“現有的Dual EC DRBG用戶儘快切換到其餘三個算法。”
MIFARE Crypto-1
Crypto-1是由NXP開發的用於MIFARE晶片的加密系統。作為專有系統，其算法最初並未公布。根據對晶片的逆向工程，來自維吉尼亞大學與Chaos Computer Club的研究人員發現了針對Crypto-1中隨機數發生器的初始化不良漏洞。
Debian OpenSSL
2008年五月，安全研究員Luciano Bello透漏了一項發現，關於2006年在隨Debian GNU/Linux和其他基於Debian的發行版，例如Ubuntu，中分發的OpenSSL軟體包中隨機數生成器的變化。這些變化大大降低了生成值的熵值，使得各種安全密鑰易受攻擊。這個安全漏洞是由於Debian開發者為解決冗餘代碼的編譯器警告，隨即對OpenSSL代碼做出了這些修改，從而導致了密鑰在世界範圍內的大量重構，儘管所有人都注意到了這個問題，但可以推測出許多舊密鑰仍在使用中。受影響的密鑰類型包含SSH密鑰、OpenVPN密鑰、DNSSEC密鑰、SSL/TLS連線中使用的X.509證書密鑰材料與會話密鑰。使用GnuPG或GNUTLS生成的密鑰由於使用了不同的方法來生成隨機數而未受到影響。由非Debian系的Linux發行版生成的密鑰也未受到影響。接到報告之後，漏洞及時得到修補，但是任何仍然使用由舊代碼生成的密鑰的服務仍然是脆弱。許多軟體包當前都包含針對弱密鑰黑名單的檢查，以試圖預防使用剩餘的弱密鑰，但是研究人員仍舊陸續發現了薄弱的密鑰實現。
PlayStation 3
2010年12月，一個自稱fail0verflow的團體宣布了恢復橢圓曲線數字簽名算法（ECDSA）私鑰的方法。索尼公司使用這種私鑰來為PlayStation 3來簽名遊戲包。攻擊的可能性來源於由於索尼未能為每個簽名產生一個新的隨機數。
RSA公鑰分解
2012年，Lenstra、Hughes、Augier、Bos、Kleinjung與Wachter發布了一篇關於從網際網路收集數百萬個RSA公鑰的分析。他們僅使用了歐幾里得算法就分解了0.2%的密鑰，利用的是基於整數分解的密碼系統特有的弱點。若n=pq是一個公鑰，n′ =p′q′ 是另一個，那么如果偶然間p=p′，那么簡單計算gcd(n,n′) =p因數都是n和n′，完全破壞了兩個密鑰。一個進行過類似實驗的組織的一員Nadia Heninger說，劣質密鑰幾乎完全出現於嵌入式系統中，由兩組結果發現的共享素數問題是由於偽隨機數發生器最初做種不良，然後在第一個和第二個素數的產生之間發生了重新做種。
