階加是一種數學運算符號,是由高德納(Donald Ervin Knuth,1938~)於1997年在《電腦程式設計藝術》中提出。它的英文名稱為 termial,定義為所有小於及等於該數的正整數的和。
基本介紹
- 中文名:階加
- 外文名:Termial
- 性質:數學運算符號
- 概念:所有小於及等於該數的正整數的和
階加的概念,階加的計算方法,階加在非正整數的擴展,階加的套用,
階加的概念
階加定義為所有小於及等於該數的正整數的和,記作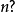 或
或  。
。
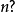

以數式表示,即有

或可以遞迴方式定義

舉例來說,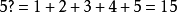 。
。
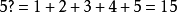
階加的計算方法
計算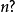 時,當
時,當 不太大時,可直接把每項相加。
不太大時,可直接把每項相加。
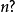

當 較大時,可使用高斯求和公式
較大時,可使用高斯求和公式


舉例來說, 。
。

階加在非正整數的擴展
一般來說,階加對於正實數以外的 ,並沒有定義。但使用公式
,並沒有定義。但使用公式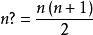 ,階加便能從正整數推廣到實數,甚至是複數。
,階加便能從正整數推廣到實數,甚至是複數。

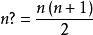
舉例來說,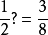 。
。
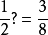
階加由高德納於1997年在《電腦程式設計藝術》中提出。這是階乘 在加法的類比,目的是闡明階乘從正整數到實數的擴展。
在加法的類比,目的是闡明階乘從正整數到實數的擴展。

階加的套用
在國小教材(北師大版)中有這樣一個問題:5個球隊比賽,每兩隊之間要賽一場,一共要賽幾場?
運用階加,我們能有算式

因此一共要賽10場。
