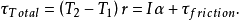基本介紹
- 中文名:阿特伍德機
- 外文名:Atwood machine
- 又譯:阿特午德機或阿特午機
- 提出:喬治·阿特伍德
- 時間:1784年
結構原理,使用範圍,等加速度的方程式,張力的方程式,非理想的滑輪,
結構原理
其基本結構為在跨過定滑輪的輕繩兩端懸掛兩個質量相等的物塊,當在一物塊上附加另一小物塊時,該物塊即由靜止開始加速滑落,經一段距離後附加物塊自動脫離,系統勻速運動,測得此運動速度即可求得重力加速度。一個理想的阿特伍德機包含兩個物體質量m1和m2,及由無重量、無彈性的繩子連結並包覆理想且無重量的滑輪。 當m1=m2,機器處於力平衡的狀態。當m2>m1,兩物體皆受到相同的等加速度。
使用範圍
阿特伍德機可以用來證明牛頓第二定律。
等加速度的方程式
我們可以藉由分解力的方法得到一個加速度的方程式。如果繩子無重量、無彈性,滑輪理想(無視半徑)且無重量,那么我們只需要考慮張力(T),還有兩個物體的重量(mg)。再來為了找出合力(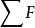 ),必須先找出個別影響兩物體的力。
),必須先找出個別影響兩物體的力。
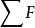
m1的力:  。
。

m2的力:  。
。


利用牛頓第二定律,我們可以得到整個系統的等加速度方程式。




阿特伍德機有時候也被用來說明拉格朗日力學中獲得的運動方程式。
張力的方程式
上述的方程式也可用來計算繩子上的張力,只需要將得到的等加速度方程式代入兩物體的力方程式之一中。

例如代入 ,我們得到
,我們得到


藉由同樣的方法,張力也可以從 中求得。
中求得。

非理想的滑輪
若m1與m2之間的重量差距很小時,滑輪的半徑(r)造成的轉動慣量(I)則不可以被忽略。
滑輪的角加速度可以從以下算式求得:

在此情況下,系統的總力矩為: