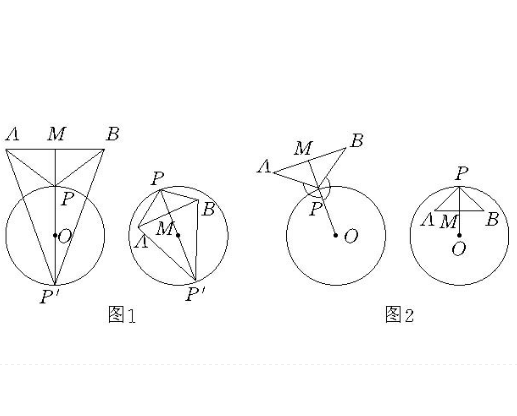
阿爾哈遜問題二（Alhazen problem Ⅱ）一般簡稱阿爾哈遜問題，是與圓有關的極值問題。若P為已知圓周上一動點，A，B為二定點，問P位於何處，可使：1.PA+PB，2.PA+PB為極大或極小。
基本介紹
- 中文名：阿爾哈遜問題二
- 外文名：Alhazen problem Ⅱ
- 所屬學科：數學
- 所屬問題：平面幾何（圓）
- 提出者：阿爾哈岑( al-Haitam Alhazen)
基本介紹,相關介紹,解決方法,
基本介紹
阿爾哈遜問題二簡稱阿爾哈遜問題(Alhazen’s problem)也被稱為阿爾哈森問題、阿爾哈岑問題、打子彈問題、Alhazen子彈問題等，指在平面上給定兩個點，要在給定的圓周上求一個點，使得它到所給兩個點的距離之和為最大或最小。這是阿拉伯物理學家兼數學家阿爾哈森(Alhazen，生年不詳，歿於1039年)在其巨著《光學集錦》(Kitab al-manazer)中所提出的問題。
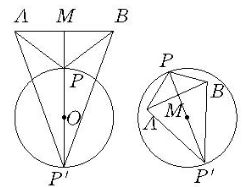
圖1
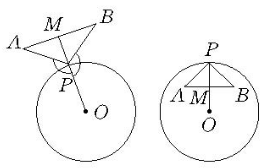
圖2
相關介紹
“打彈子問題”這個數學名題，都說是阿拉伯數學家阿爾哈岑( al-Haitam Alhazen，約965~1039)首先提出來的其實，這個問題的實質性內容確是阿爾哈岑提出的，但“打彈子”的形式是後來人加上去的。
阿爾哈岑是阿拉伯穆斯林學者中很有影響的一個物理學家，出生在南伊拉克的巴斯拉，擅長機械設計，曾宣稱要製造一台調節尼羅河泛濫的機械，他對光學也很有研究，寫過一本《光學》的著作，所謂“打彈子問題”就是這本書里提出來的，原文的敘述是這樣的：“在一個球形凹面鏡上找出一個點，使由一個已知點射來的光線被反射到另一個已知點去。”這是幾何光學的問題，若抽象成一個數學題目，可這樣表述：“在一個已知圓內，作出一個其兩腰通過圓內兩個已知點的等腰三角形。"後來的一系列著名數學家都參與這個問題的研究，大家發現，阿爾哈岑提出的問題可以用形象的打彈子形式來表達，這個源出光學的問題，就變成了“阿爾哈岑彈子問題”：
一張圓形彈子檯上有兩隻彈子球，用什麼方法打擊一球，使其從彈子檯橡皮邊緣彈回時必定撞擊另一個球?”
解決方法
求解這個問題的關鍵是要利用光學上人射角等於反射角的原理。如圖3，設圓O內有A、B兩點，P為圓周上所要求的一點，以O為原點建立直角坐標系，設A、B的坐標分別為
，P的坐標為(x,y)，只要P的坐標確定了，這個問題也就解決了。
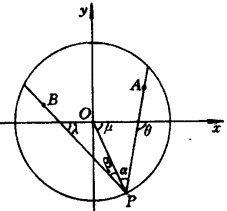
圖3
設PA、PO、PB與x軸的交角分別為θ、μ、λ，PA與PO、PB與PO的交角分別為α、β，根據光學反射定律，
而α=θ-μ，β=μ-λ，
由
得
因為P(x,y)在圓O上，由圓的方程，可得
因此，上式可化為
.
此方程代表一條雙曲線，因此，最終答案是，所求P點由圓和雙曲線的交點決定。由於一個圓和一條雙曲線一般有四個交點，所求點P就可能有4個位置，這和由圓的方程與雙曲線方程組成的二元二次方程組可以有4組解相一致。
從極值的角度來分析，阿爾哈岑彈子問題可以這樣敘述：“在一個圓的圓周上找出一個點，使其與圓內兩個已知點的距離之和最小(或最大)。”
阿爾哈岑曾對圓內兩點和圓心距離相等的特殊性作過研究，他得出的結論是：已知圓和通過兩已知點及已知圓圓心的圓的交點是已知圓上到這圓內兩已知點距離之和最小的點。
同時阿爾哈岑還研究了這樣的問題：怎樣去擊一個圓檯球桌上的彈子球，使其兩次碰邊緣後仍回到原位。如圖4，P為彈子球的原位，撞擊後，到P'點，P'點彈出至P”點，P”點再彈回到P，要達到這個目的，關鍵是要選準P'的位置。
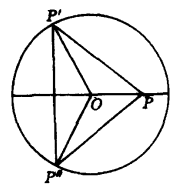
圖4
