基本介紹
- 中文名:阿拉巴馬悖論
- 基本原則:公平合理
- 時間:1792年
- 原理:選票按人數比例分配
簡介,實例說明,
簡介
美國國會的議員是按州分配。假定美國的人口數是p,各州的人口數分別是p1,p2,Λ,pl。再假定議員的總數是n,記:
稱它為第i個州分配的份額.漢密爾頓方法的具體操作如下: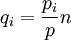
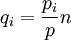
(1) 取各州份額qi的整數部分[qi],讓第i個州先擁有[qi]個議員。
(2) 然後考慮各個qi的小數部分{qi},按從大到小的順序將餘下的名額分配給相應的州,直到名額分配完為止。
漢密爾頓方法看起來十分合理,但是仍存在問題。按照常規,假定各州的人口比例不變,議員名額的總數由於某種原因而增加的話,那么各州的議員名額數或者不變,或者增加,至少不應該減少,可是漢密爾頓方法卻不能滿足這一常規。1880年,阿拉巴馬州曾面臨這種狀況,人們把漢密爾頓方法產生的這一矛盾叫作阿拉巴馬悖論。
這個問題從誕生之日起,就一直吸引著眾多政治家和數學家去研究。這裡要特別提出的是,1952年數學家阿羅證明了一個令人吃驚的定理——阿羅不可能定理,即不可能找到一個公平合理的選舉系統。這就是說,只有相對合理,沒有絕對合理。原來世上本無“公”!阿羅不可能定理是數學套用於社會科學的一個里程碑。
實例說明
假定某學院有三個系,總人數是200人,學生會需要選舉20名委員,表1是按漢密爾頓方法進行分配的結果。
表1:
系別 | 人數 | 所占份額 | 應分配名額 | 最終分配名額 |
甲 | 103 | 51.5 | 10.3 | 10 |
乙 | 63 | 31.5 | 6.3 | 6 |
丙 | 34 | 17 | 3.4 | 4 |
合計 | 200 | 100 | 20 | 20 |
由於考慮到20個委員在表決提案時會出現10:10的結局,所以學生會決定增加1名委員。按照漢密爾頓方法分配名額得到表2。
表2:
系別 | 人數 | 所占份額 | 應分配名額 | 最終分配名額 |
甲 | 103 | 51.5 | 10.815 | 11 |
乙 | 63 | 31.5 | 6.615 | 7 |
丙 | 34 | 17 | 3.570 | 3 |
合計 | 200 | 100 | 21 | 21 |
表2的例子指出,委員的名額增多了,但丙系反而減少一名,令丙系不能接受!
