阿基米德折弦定理

阿基米德（Archimedes，公元前287～公元前212年，古希臘）是有史以來最偉大的數學家之一。他與牛頓、高斯並稱為三大數學王子。如果以他們三人的宏偉業績和所處的時代背景來比較，或拿他們影響當代和後世的深邃久遠來比較，還應首推阿基米德。他甚至被人尊稱為“數學之神”。

英國人希思（T?L?Heath，1861～1940）編的《阿基米德全集》未見收錄，當然我國在1998年根據希思本由朱恩寬、李文銘譯，葉彥潤、常心怡校的中文版《阿基米德全集》（陝西科技出版社）也就沒有收錄阿基米德折弦定理。（雖然這本全集中未收錄折弦定理，但一些競賽書上還是給予了介紹）

阿拉伯Al-Biruni（973年～1050年）的譯文中保存了阿基米德折弦定理的內容，蘇聯在1964年根據Al-Biruni本出版了俄文版《阿基米德全集》，第一題就是阿基米德折弦定理。

阿基米德折弦定理：一個圓中一條由兩長度不同的弦組成的折弦所對的兩段弧的中點在較長弦上的射影，就是折弦的中點。

如圖中所示，AB和BC組成圓的折弦，AB>BC，M是弧ABC的中點，MF⊥AB，垂點為F。則AF=BF+BC

基本介紹

• 中文名：阿基米德折弦定理
• 提出者：阿基米德
• 套用學科：數學
• 適用領域範圍：幾何

定理定義

如右圖所示，AB和BC是⊙O的兩條弦（即ABC是圓的一條折弦），BC>AB，M是弧ABC的中點，則從M向BC所作垂線之垂足D是折弦ABC的中點，即CD=AB+BD。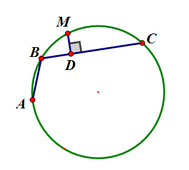

定義：從圓周上任一點出發的兩條弦，所組成的折線，我們稱之為該圖的一條折弦。

驗證推導

該定理常規的證明方法有以下三種：

方法1：補短法

如圖，延長DB至F，使BF=BA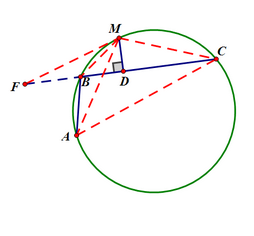

∵M是弧ABC的中點

∴∠MCA=∠MAC=∠MBC

∵MBAC四點共圓

∴∠MCA+∠MBA=180°

∵∠MBC+∠MBF=180°

∴∠MBA=∠MBF

∵MB=MB,BF=BA

∴△MBF≌△MBA

∴∠F=∠MAB=∠MCB

∴MF=MC

∵MD⊥CF

∴CD=DF=DB+BF=AB+BD

方法2：截長法

如圖，在CD上截取DG=DB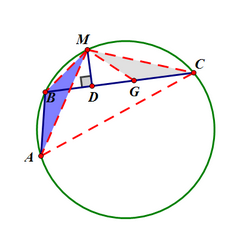

∵MD⊥BG

∴MB=MG，∠MGB=∠MBC=∠MAC

∵M是弧ABC的中點

∴∠MAC=∠MCA=∠MGB

即∠MGB=∠MCB+∠BCA=∠MCB+∠BMA

又∠MGB=∠MCB+∠GMC

∴∠BMA=∠GMC

∵MA=MC

∴△MBA≌△MGC（SAS）

∴AB=GC

∴CD=CG+GD=AB+BD

方法3：垂線法

如圖，作MH⊥射線AB，垂足為H。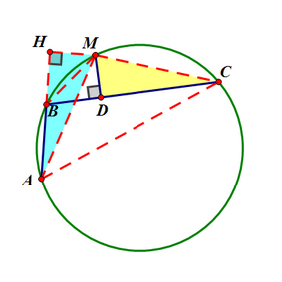

∵M是弧ABC的中點

∴MA=MC

∵MD⊥BC

∴∠MDC=90°=∠H

∵∠MAB=∠MCB

∴△MHA≌△MDC（AAS）

∴AH=CD，MH=MD

又∵MB=MB

∴Rt△MHB≌Rt△MDB（HL）

∴HB=BD

∴CD=AH=AB+BH=AB+BD

定理推廣

推論

推論1

推論1：設M是弧AC的中點，在弧AM上取一點B，連線AB、MB、MC、BC，那么MC²-MB²=BC*AB

證明：如圖，作MD⊥BC，由勾股定理得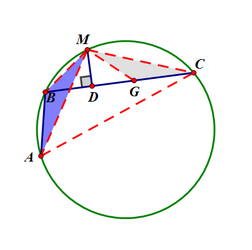

MC²=CD²+MD²

MB²=BD²+MD²

∴MC²-MB²=CD²-BD²=（CD+BD）（CD-BD）=BC*AB

推論2

推論2：設M是弧AC的中點，B在圓上，且在弧AMC外。連線AB、AC、MB、MC，那么MB²-MC²=AB*BC

證明：如圖，取弧ABC的中點N，連線MN
　　

由推論1可知AB*BC=NC²-NB²

∵M是弧AC的中點，易得弧CN=弧ABC/2，弧CM=弧AC/2

且弧ABC+弧AMC=圓周360°

∴弧CN+弧CM=弧MN=180°

∴MN是直徑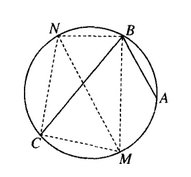

∵C、B在圓上

∴∠MCN=∠MBN=90°

勾股定理得NC²+MC²=NB²+MB²=MN²

∴NC²-NB²=MB²-MC²=AB*BC

逆定理

設D是△ABC邊BC上一點，且AB+BD=CD。作△ABC的外接圓，有如下逆定理：

逆定理1

取弧ABC的中點M，連線MD，則MD⊥BC。

證明：不妨作MD‘⊥BC於D’，根據定理有AB+BD‘=CD’

∵AB+BD=CD

∴CD'-BD'=CD-BD=AB

∴D與D'重合

∴MD⊥BC

逆定理2

作DM⊥BC交弧ABC於M，則M是弧ABC的中點。

證明：不妨取弧ABC中點M'，由逆定理1可知M'D⊥BC

∵MD⊥BC，且M在弧ABC上

∴M與M’重合

∴M是弧ABC的中點