基本介紹
解釋



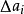



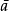














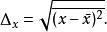






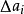



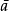














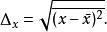


在量子力學中,量子漲落(英語:quantum fluctuation。或量子真空漲落,真空漲落)是在空間任意位置對於能量的暫時變化。從維爾納·海森堡的不確定性原理可以推導出這結論。...
量子泡沫也叫時空泡沫(spacetime foam),是惠勒(John Wheeler)1955年根據量子力學提出的概念,所以又叫惠勒泡沫。量子泡沫即為誕生前宇宙的概念化。在量子泡沫的普朗克...
量子相變是指發生在絕對零度的相變現象。與熱相變不同的是,熱相變的發生是由於熱擾動所造成,而量子相變是經由量子漲落所造成。量子相變的發生代表著在量子多...
圈量子引力的主要物理構想都以廣義相對論和量子力學為基礎, 而不附加任何額外的結構。作為一個數學上嚴格的不依賴於背景的理論框架, 它成功地貫徹了廣義相對論的...
圈量子引力論(loop quantum gravity,LQG),又譯迴圈量子重力論,英文別名圈引力(loop gravity)及量子幾何學(quantum geometry);由阿貝·阿希提卡(Ahbay Ashtekar)、...
台北時間2014年3月3日,德國和美國的物理學家們宣布發現了一種新的粒子類型,他們將其稱之為量子滴(dropleton)。在這篇發表在期刊《自然》上的文章里,科學家們...
量子光學是套用輻射的量子理論研究光輻射的產生、相干統計性質、傳輸、檢測以及光與物質相互作用中的基礎物理問題的一門學科。量子光學一詞是在有了雷射後才提出來的...
量子成像是量子光學的一個重要分支,是研究在光場量子特性下所能達到的光學成像極限的問題。不同於經典成像,量子成像是利用光場的量子力學性質和其內稟並行特點,在...
在當代量子物理學中,量子真空被定義為其方程既遵守波動力學也遵守狹義相對論的系統的最低能量狀態。然而,它不只是一種系統的狀態,它也是神秘的“零點能”場(“...
量子宇宙學(quantum cosmology)是將量子物理學套用於宇宙起源 研究的試探性理論。按照廣義相對論,在時間的起始時刻必有一個奇點。但像所有經典物理理論一樣,廣義相對...
循環量子引力理論,即圈量子重力論(loop quantum gravity,LQG),又譯迴圈量子引力論,英文別名圈引力(loop gravity)、量子幾何學(quantum geometry);由阿貝·阿希提卡...
