基本介紹
- 中文名:重力潮汐改正
- 外文名:correction of gravity measurement for tide
- 學科:測繪科學
- 定義:日月引力引起潮汐形變的重力改正
- 影響因素:重力固體潮、海潮負荷效應
- 改正方法:重力固體潮改正、海潮負荷改正
影響因素,重力固體潮,海洋潮汐的負荷效應,改正方法,重力固體潮模型改正,海潮負荷模型改正,重力潮汐改正模型,模型的建立,模型的精度分析,
影響因素
重力固體潮
重力固體潮主要來自於日、月天體(非常微小的部分來自於離地球較近的行星)的引潮力的作用,是地表重力時間變化的主要成份。採用現代天文觀測技術獲得的太陽、月亮和行星的精密軌道參數,可以獲得精確的引潮位展開表。因此,一方面,根據描述地球彈性及其對引潮力回響特徵的Love數和各類體潮的潮汐參數,可以從理論上預測出重力固體潮。研究表明,由於近周日共振的影響,周日頻段的固體潮潮汐參數表現出非常顯著的頻率依賴特徵;對於任何潮波,重力潮汐參數可以表示為全球常數項和相對極其微小的緯度依賴項之和。在固體潮理論模擬中,已逐步顧及到地球的自轉、橢率、地幔的非彈性、側向(密度)非均勻性及(彈性)各向異性等特徵。研究表明,側向非均勻性和各向異性對固體潮的影響很小,在目前的技術條件下無法在實際觀測結果中反映出來。同時,必須看到,這些理論模擬結果都是基於流體靜力平衡假設獲得的,這一假設將直導致採用的液核動 力學橢率偏小約5%,從而導致重力潮汐,特別是周日潮汐模擬計算結果存在比較大的偏差;為此,科學家避免了流體靜力平衡假設,採用實際觀測資料修正液核動力學橢率,獲得更精確的重力潮汐理論模型。另一方面,重力固體潮可以通過高精度重力儀在地表的長期連續觀測獲得。觀測結果表明,隨著觀測技術的提高,特別是超導重力儀和 LaCoste-ET 彈簧重力儀在全球範圍內的普遍使用和觀測資料的長期積累,重力固體潮的觀測精度已經非常高;目前的重力潮汐理論模型可以很好地解釋觀測結果,特別是超導重力儀觀測結果,二者在主要潮波的差異優於0.5%。採用全球超導重力儀長期連續觀測資料,考慮周日潮汐的近周日共振特徵,建立了高精度的重力潮汐全球實測模型。
海洋潮汐的負荷效應
海潮的負荷(OTL)效應是地表潮汐觀測和潮汐理論模擬之間差異的主要來源,由於海潮和固體潮具有相同的力源和類似的頻譜特徵,只能採用表面負荷理論和已有的海潮模型,通過表面負荷 Green函式與海潮潮高的全球褶積從理論上計算出海潮的負荷影響。1980年,Schwiderski採用大量驗潮站資料和潮汐運動方程,建立了第一個全球海潮模型。隨著衛星測高資料的積累及數值計算技術的發展,特別是有限元數值計算方法的套用,獲得了 許多精度和解析度更高的全球海潮模型。大量地表重力潮汐觀測結果表明,儘管目前全球海潮模型的精度和空間解析度存在著差異,但是對負荷效應的模擬計算結果影響甚微,在目前的觀測精度以內。對於中國大陸,局部海域的海潮負荷對重力觀測,特別是沿海地區重力觀測的影響極其顯著,中國大陸具有很長的海岸線,要建立中國大陸精密的重力潮汐改正模型必須顧及局部近海海潮運動特徵。
採用理論或實驗固體潮模型、海潮負荷效應,可以精確合成重力觀測中的潮汐變化,為連續、流動和絕對重 力觀測提供精密的潮汐改正模型。
改正方法
重力固體潮模型改正
對於某個地球模型,採用合理的數值積分方法,解算地球潮汐運動方程,獲得重力潮汐參數。由於地球自轉和橢率,二階重力潮汐參數可以表示為常數項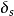 和微小的緯度依賴項
和微小的緯度依賴項 、
、 之和。事實上,地球的高階重力潮汐參數也存在緯度依賴項,但由於地球的潮汐形變最主要的部分是二階項,高階潮汐信號相對較小,且緯度依賴項非常微弱,在現有觀測技術條件下可忽略。Dehant等學者採用分層(包括地幔、內外核、不包含大氣和海洋)、自轉、微橢、非彈性地球模型和非流體靜力平衡的地球模型,考慮了內部的橢率對密度、剪下和壓縮模量、重力位以及邊界地形的影響,為了使得計算得到的理論自由核章動(FCN)周期接近於觀測值,考慮了地幔的對流和非彈性,理論模擬了重力潮汐參數 (模 型 記 為 DDW99)。Mathews等學者採用基於 VLBI觀測獲得的FCN 周期,修正了 PREM 模型的液核和地球的動力學扁率,並將 Love數和重力潮汐參數描述為若干旋轉簡正模共振之和的形式,獲得了另一個精確的重力潮汐理論模型 (記為 M2001)。與以前的同類研究結果相比,由於這兩個模型採用實際觀測的FCN 周期修正液核的動力學扁率,從客觀上避免了流體靜力平衡近似,由此獲得的重力潮汐參數更客觀地描述了近周日共振特徵,被認為是目前最精確的兩個潮汐理論模型.
之和。事實上,地球的高階重力潮汐參數也存在緯度依賴項,但由於地球的潮汐形變最主要的部分是二階項,高階潮汐信號相對較小,且緯度依賴項非常微弱,在現有觀測技術條件下可忽略。Dehant等學者採用分層(包括地幔、內外核、不包含大氣和海洋)、自轉、微橢、非彈性地球模型和非流體靜力平衡的地球模型,考慮了內部的橢率對密度、剪下和壓縮模量、重力位以及邊界地形的影響,為了使得計算得到的理論自由核章動(FCN)周期接近於觀測值,考慮了地幔的對流和非彈性,理論模擬了重力潮汐參數 (模 型 記 為 DDW99)。Mathews等學者採用基於 VLBI觀測獲得的FCN 周期,修正了 PREM 模型的液核和地球的動力學扁率,並將 Love數和重力潮汐參數描述為若干旋轉簡正模共振之和的形式,獲得了另一個精確的重力潮汐理論模型 (記為 M2001)。與以前的同類研究結果相比,由於這兩個模型採用實際觀測的FCN 周期修正液核的動力學扁率,從客觀上避免了流體靜力平衡近似,由此獲得的重力潮汐參數更客觀地描述了近周日共振特徵,被認為是目前最精確的兩個潮汐理論模型.
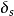


海潮負荷模型改正
目前的研究表明 不同全球海潮模型在遠海區比較一致,而差別主要反應在沿海地區,因此為了提高沿海測點的海潮負荷計算精度,遠區可採用 NAO99 (格線0.5°×0.5°)全球海潮模型,近區可採用 Fang等學者提供的中國近海潮汐資料。海潮負荷影響主要在沿海地區,海潮負荷影響在南部沿海區域為最大, 達到 ·
· ,在其他沿海區域也在
,在其他沿海區域也在 ·
· 左右,其中局部近海潮汐的影響約占 10%,次要潮波的影響約占3%,在高精度重力測量 中都有必要充分考慮;隨著離海岸線距離的增加,海潮負荷的影響逐步減小。
左右,其中局部近海潮汐的影響約占 10%,次要潮波的影響約占3%,在高精度重力測量 中都有必要充分考慮;隨著離海岸線距離的增加,海潮負荷的影響逐步減小。




重力潮汐改正模型
模型的建立
重力潮汐包含了固體地球的潮汐以及由海洋潮汐引起的負荷潮汐,並耦合在實際的重力觀測中(如相對和絕對重力測量),因此重力觀測資料中的潮汐改正就是扣除這兩部分的影響.固體潮模型給出的是頻率域各潮波的潮汐參數,也就是潮波的振幅與剛體地球潮波振幅的比值以及潮波的相位與剛體地球潮波的相位之間的差值。潮波的振幅總是正的,由於海潮模型給出的潮高和相位不包含類似於固體潮中的大地係數的量,因此所計算的海潮負荷也沒有與大地係數有關的項,而固體潮計算中的大地係數在不同的緯度地區有正負之分,最後用振幅和相位來表示將導致相位180°的偏移,因此在將海潮負荷和固體潮模型值疊加時需考慮由此引起的相位的改正,不同緯度區的相位改正值可參考文獻。因此,對於中國及周邊地區,只有長周期潮汐存在相位改正的問題,即在緯度大 於 35.26°的 地 區 要 加 上180°的相位改正。因此最後潮汐改正所用的潮汐參數就是綜合固體潮模型值和海潮負荷值:

式中 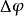 為相位改正值。由於三階和四階的固體潮潮波振幅很小,因此只有二階的潮波加上了海潮負荷的影響,也就是說在某一個波群中,二階的潮波採用顧及海潮負荷影響的潮汐參數,而三階和四階的潮波採用理論的潮汐參數。對於中國大陸任何測點,採用理論或實驗模型(DDW99,M2001)即可獲得重力潮汐參數;根據海潮模型(包括 NAO99,FES04 和中國近海海潮圖)提供的各主要潮波的等潮圖(振幅和相位),根據表面負荷理論計算它們的負荷效應,然後利用上式對潮波的重力潮汐參數進行修正;
為相位改正值。由於三階和四階的固體潮潮波振幅很小,因此只有二階的潮波加上了海潮負荷的影響,也就是說在某一個波群中,二階的潮波採用顧及海潮負荷影響的潮汐參數,而三階和四階的潮波採用理論的潮汐參數。對於中國大陸任何測點,採用理論或實驗模型(DDW99,M2001)即可獲得重力潮汐參數;根據海潮模型(包括 NAO99,FES04 和中國近海海潮圖)提供的各主要潮波的等潮圖(振幅和相位),根據表面負荷理論計算它們的負荷效應,然後利用上式對潮波的重力潮汐參數進行修正;
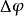








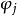
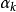

最後利用上述方程就可以獲得該測點的潮汐改正值,從而獲得中國大陸的重力潮汐改正模型。海潮負荷使得中國大陸,特別在沿海區域重力潮汐的影響幅度的形態發生了顯著的變化,海潮負荷影響最大的位於南部沿海區域,且隨著離海岸線距離的增加,影響逐漸減小。
模型的精度分析
採用 DDW99固體潮模型和海潮負荷對武漢台超導重力儀連續觀測作重力潮汐改正,分析表明經重力潮汐改正後,超導重力儀觀測與局部氣壓變化存在極強的相關性,重力變化來源主要是局部的環境變化,如果扣除局部氣壓的影響和長期趨勢項,基本上不包含重力潮汐變化或潮汐信號非常微弱,其均方差僅為 ·
· 。
。



