重力井

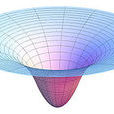
重力井或引力井是在空間中圍繞著某個天體的引力場的概念模型。好比在一塊撐著的布上放上一塊鐵球，鐵球周圍的布就向下凹陷，同樣，大質量的天體也能令周圍的空間產生類似的凹陷，周圍的小天體會向凹陷里陷落，引力或許就是這樣產生的。

基本介紹

• 中文名：重力井
• 外文名：Gravity well

重力井（Gravity well）

重力井或引力井是在空間中圍繞著某個天體的引力場的概念模型。天體質量越大，重力井越深，範圍越大。

好比在一塊撐著的布上放上一塊鐵球，鐵球周圍的布就向下凹陷，同樣，大質量的天體也能令周圍的空間產生類似的凹陷，周圍的小天體會向凹陷里陷落，引力或許就是這樣產生的。

相對於太陽系中的其他天體，太陽是非常巨大的，因此，圍繞它的相應的重力井會表現的比較深，延伸的比較遠。相反的，小行星和小衛星的重力井會被描述的非常淺。行星或月球表面的所有東西被認為是在天體的重力井的底部，因此逃離行星和月球重力井的影響有時被稱作“爬出重力井”。重力井越深，空間束縛的“攀爬者”就需要耗費更多的能量來逃離它。在天體物理學中，重力井是一種圍繞大質量天體的特別的引力勢場。其他種類的勢能井包括電勢能井和磁勢能井。重力井的物理模型有時被用來說明軌道力學，重力井被頻繁的與廣義相對論中的嵌入圖相混淆，但是這兩個概念是明顯分離的，而非直接相關。

詳細資訊（Details）

如果G這個萬有引力常數為（ ）,那么一個質量為M的球對稱物體的外部引力勢由下列公式得出：

右邊圖中顯示的是二維函式的圖，這個圖由與 成比例的內勢作成，與均勻密度的物體相對應，但由於這個實驗粒子不能與物體相交，這種內勢一般是不相關的。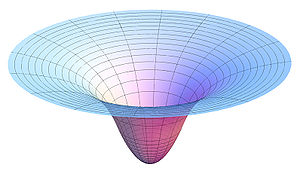

重力井模型

勢函式有一個雙曲線的橫截面；中心的突然下沉是“重力井”的起源，黑洞就沒有這個“閉合”下沉，因為它的大小隻取決於它的視界。

物理學重力井（Physical Gravity well）

圖1

在一個均勻的引力場中，一個點的引力勢與高度成正比。因此引力勢Φ(x,y)被構造為一個物理表面放置在均勻引力場中，實際點在−Φ方向，然後表面上的每個點會有一個實際的重力勢能，它與在這一點的Φ值成正比。因此，一個被限制在這個表面上移動的物體會有大致相同的運動方程來描述物體在勢場Φ本身中的移動。

右邊圖1：這張圖片顯示了重力井的四個軌跡分類，勢能用黑色表示，運動物體的動能用紅色表示，根據克卜勒定律關聯的變化速度隨著距離變化。

右邊圖2：這張圖片顯示了重力與重力向量場是休戚相關的。這表明這只是一個二維切片的重力場中重力。z軸不再是一個空間維度,而是代表能量。

重力井基於這一原則上被建造，可以在許多科學博物館裡看到模型。

在這個模型中有幾個來源不準確：

● 物體與表面之間的摩擦在真空中沒有類似的模擬。這種效果可以通過使用滾動球代替滑動塊來減弱。

圖2

●物體的垂直運動產生的動能沒法模擬，這種效果可以通過製造較淺的重力井來減弱（即通過選擇較小的Φ軸縮放因子）

●一個滾動球的動能沒法模擬。這種效果可以通過使球的質量接近它的中心，以至於在某個瞬間的慣性比mr²小。

●球的質量中心不位於表面，而是在一個固定的距離r上，它的勢能變化取決於在該點的表面的斜率。對於一個固定大小的球，這種效果可以通過構建表面而消除，因此是球的中心而不是表面本身依賴於圖Φ。

橡膠板模型（The rubber-sheet model）

考慮一個具有標準片材理想化的橡膠板懸浮在一個統一的重力場中，處於平衡中，每一部分的彈性張拉必須與該片的一部分的重力拉力相等，即是：

其中K是橡膠的彈性常數，h(x)是片向上的位移（假定比較小），g是引力場的強度，ρ(x)是板片的質量密度。

質量密度可以被看做是固有的，或屬於附在板片頂部的物質。這種平衡條件與引力泊松方程在形式上是相同的。

Φ(x)是引力勢，ρ（x）是質量密度。因此，粗略的講，一個巨大的物體放置在橡膠板，會使橡膠板形成正確的重力變形，（在剛性的情況下）把第二個測試對象放置在第一個附近，在重力作用下將接近正確的受力定律。

重力井與廣義相對論（Gravity wells and general relativity）

右邊圖3：一種描述廣義相對論曲率空間的嵌入圖。雖然相似,但這並不描繪太陽的引力井。

圖3

剛性重力井和橡膠板模型這兩個模型經常被誤認為是廣義相對論的模型。由於與廣義相對論的嵌入圖表偶同 [需要引證]，也許愛因斯坦把自己的重力曲率彎曲光路的工作描述為了廣義相對論的預測。尤其是嵌入圖在教科書（在歐幾里德三維空間中等距嵌入一個史瓦西度規的常量時間赤道片）中常被使用，看上去類似於重力井。

然而，從根本上嵌入圖在許多方面都不同於重力井。最重要的是，嵌入圖是一個圖形，而勢能圖有一個顯著的“向下”的方向；因此可以使重力井“倒掛”（通過否定勢能）轉為斥力。然而把一個史瓦西嵌入倒置（通過旋轉它）卻沒有影響，因為它可以使自己的內在幾何形狀不變。在史瓦西表面的測地線彎向中心塊體就像球在重力井中滾動。對於斥力場，史瓦西嵌入沒法模擬：但在這樣一個場裡可以在廣義相對論中獲得模型，特別的集合形狀不能嵌入在三個維度里。

史瓦西嵌入通常用雙曲線截面來繪製，像一個勢能井。但事實上它有一個拋物截面，不像重力井，是不接近平面的漸近線。