配合度檢驗(goodness of fit test)主要用於檢驗單一變數的實際觀察次數分布與某理論次數是否有差別。由於它檢驗的內容僅涉及一個多因素項分類的計數資料,也可以說它是一種單因素檢驗(one-way test)。
基本介紹
- 中文名:配合度檢驗
- 外文名:goodness of fit test
- 別稱:單因素檢驗
簡介
統計假設

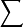
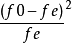
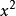
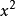
配合度檢驗(goodness of fit test)主要用於檢驗單一變數的實際觀察次數分布與某理論次數是否有差別。由於它檢驗的內容僅涉及一個多因素項分類的計數資料,也可以說它是一種單因素檢驗(one-way test)。

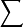
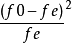
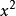
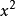
配合度檢驗(goodness of fit test)主要用於檢驗單一變數的實際觀察次數分布與某理論次數是否有差別。由於它檢驗的內容僅涉及一個多因素項分類的計數資料,也可以說它...
《21世紀高職高專規劃教材·機械基礎系列:公差配合與檢測》的內容包括緒論,孔、軸的公差與配合,幾何公差,尺寸公差與幾何公差的關係,表面粗糙度,測量技術基礎,幾何...
《公差配合與精度檢測》按照教育部倡導的“以就業為導向,以能力為本位”的職業教育改革精神,結合作者多年來開展的公差配合與精度檢測課程改革成果進行編寫。以企業...
主要內容包括尺寸公差及配合設計、形位公差設計、表面粗糙度設計、光滑工件尺寸檢測、典型零件公差及檢測、尺寸鏈分析與計算等。全書採用最新的國家標準,內容通俗易懂,...
《公差配合與檢測技術》是2007年人民郵電出版社出版的圖書。本書以貫徹國家最新...4.6 形位誤差的檢測思考題與習題第5章 表面粗糙度與檢測5.1 概述...
《公差測量與配合》從互換性生產要求出發,主要內容包括互換性與標準化、測量技術基礎、光滑圓柱結合的公差與配合、形位公差及其檢測、表面粗糙度及其檢測、圓錐公差及...
《公差配合與精度檢測實訓指導》是2009年電子工業出版的圖書,作者是趙姝娟、...全書共分七部分,包括緒論,長度的檢測,形狀和位置誤差的檢測,表面粗糙度的檢測,...
《公差配合與檢測技術基礎》重點介紹公差配合與檢測技術基礎的基本術語、基本理論和基本知識。全書內容包括緒論、公差與配合、形位公差與檢測、表面粗糙度、公差配合...
本教材共分9章,分別為緒論,極限與配合及檢測,形狀和位置公差及檢驗,表面粗糙和測量,測量技術基礎,光滑極限量規,鍵、花鍵的公差及檢測,普通螺紋結合的公關及檢測,...
《公差配合與測量技術》內容包括:緒論,光滑圓柱的公差與配合,測量技術基礎,光滑極限量規,幾何公差及檢測,滾動軸承公差與配合,表面粗糙度及其檢測,圓錐的公差配合與...
《公差配合與機械測量》共分8個學習情境,主要內容包括緒論、尺寸誤差檢測、形位誤差檢測、表面粗糙度檢測、錐度誤差檢測、螺紋誤差檢測、齒輪誤差檢測、量規設計與使用...
本書共12章,內容包括緒論、尺寸公差與配合、幾何公差及其測量、表面粗糙度與測量、典型零件的公差與檢測、尺寸鏈、基本測量的實際操作等。本書採用國家最新標準,側重...
全書內容包括緒論;光滑圓柱的公差與配合;測量技術基礎;形狀和位置公差及檢測;表面粗糙度及其檢測;量規設計基礎;圓錐和角度的公差與檢測;平鍵、花鍵聯結的公差與檢測;...
本手冊可供從事機械設計、工藝、檢驗和標準化工作的人員使用,也可供大專院校師生...6 配合面的表面粗糙度884 四、滾動軸承公差新舊國家標準的對照885 五、滾動...
《公差配合與技術測量》是化學工業出版社2004年出版圖書。作者是劉越。本書主要內容包括極限與配合、測量技術基礎、形狀和位置公差、表面粗糙度及測量、光滑極限量規、...
本書共11章,內容包括緒論、尺寸公差與配合、技術測量基礎、形位公差及其測量、表面粗糙度與測量、典型零件的公差與檢測、尺寸鏈、基本測量的實際操作等。...
本書以機械製造業工廠現場零件的幾何量檢測為主線,全面的介紹了幾何量的互換性...及其尺寸檢測、幾何公差及檢測檢測、表面粗糙度及其檢測、圓錐的極限與配合及角度...
[1] 本書總共設定五個工作項目,分別為光滑圓柱公差配合及其檢測、測量技術基礎、幾何公差及其檢測、表面粗糙度輪廓及其檢測、常用連線件的公差配合及其檢測。《公差配...
卡方統計量是由統計學家皮爾遜於1900年提出的用於檢驗實際分布與理論分布配合程度,即配合度檢驗的統計量。它是由各項實際觀測次數( )與理論分布次數( )之差的平方...
