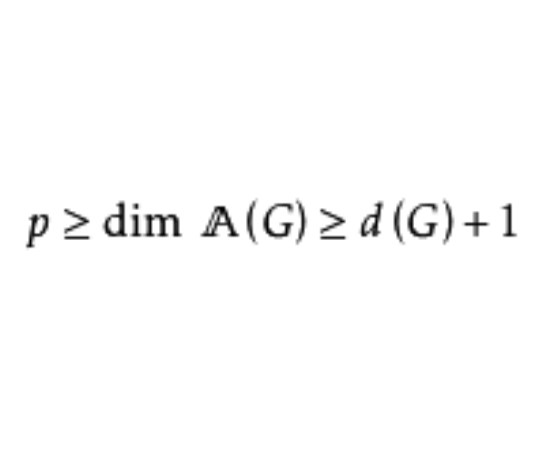鄰接代數

鄰接代數(adjacent algebra)是與圖的鄰接陣關聯的一類代數，以圖G的鄰接矩陣A的多項式(即A的冪的線性組合)為元素構成的代數，記為A(G)，這個代數作為復向量空間，其維數是有限的，其維數的下界為圖的直徑d加1。

基本介紹

• 中文名：鄰接代數
• 外文名：adjacent algebra
• 所屬學科：數學
• 所屬問題：組合學(圖與超圖)
• 簡介：與圖的鄰接陣關聯的一類代數

基本概念

如果B是一個n×n矩陣，那么由B產生的代數定義為I，B，B²，…的所有線性組合的集合。換句話說，由B產生的代數是一個關於矩陣B的矩陣多項式集合。如果圖G的鄰接矩陣為A，那么由A產生的代數被稱為G的鄰接代數(adjacency algebra)。

也可以說圖G的鄰接矩陣的各個複數係數的多項式在通常的矩陣運算法則下構成一個有限維的線性空間，它也是一個代數，稱為圖G的鄰接代數，記作 。用圖G的點數和直徑可以給出鄰接代數的維數的界。

相關定理

定理 連通p階圖G的鄰接代數的維數 滿足不等式

其中d(G)是G的直徑。

證明 左邊的不等式可由A(G)是p階方陣及凱萊-哈密頓(Cayley-Hamilton)定理得到。

為證右邊的不等式，只要證 是線性無關的即可，其中A=A(G)。

記 ，不妨設 ，且 是G中聯結 和 的一條長度為d的測地線，d<p，於是， ， 的 元 在 時為零，而 。

若存在一個線性組合

而 不全為零，不妨設 是下標最大的非零係數， ，考慮上式左邊的(1，j)元，得

得到矛盾，故 是線性無關的。證畢。

正則圖的鄰接代數

利用鄰接代數，Hoffman刻畫了正則圖的特性，並給出了以下結論。全1矩陣用符號J來表示。

定理 設G是一個有n個頂點的圖，那么若且唯若J是在G的鄰接代數中時，G才是一個連通的正則圖。