邵劍夫銳直線(Sorgenfrey line)實數集R上的一種拓撲結構.以R上所有右半開區間
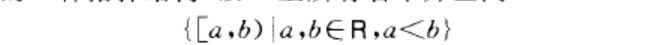
為子基的拓撲空間,稱為邵劍夫銳直線,其拓撲稱為右半開區間拓撲.這種拓撲首先出現在亞歷山德羅夫(AnexcaH,-epos, }1. C.)和烏雷松(y pbICOH , } } . C.)於1929年發表的論文中.邵劍夫銳(Sorgenfrey, R.H.)於1949年發表的論文使它成為一般拓撲學中通用的反例.它是第一可數的、遺傳可分的、完備正規、遺傳林德勒夫的、遺傳仿緊的、實冪緊的空間.但是,它不是第二可數的、連通的、可度量化的空間.自身的乘積不是正規空間.
