又稱“那塞特準則”，是對流換熱研究中藉以確定對流換熱係數的待定準則數，為一無量綱綜合量，常用符號Nu表示。其值常通過實驗或由求解相關的準則方程式而得到。Nu與無量綱溫度分布在壁面上的梯度有關,可以反映流體的導熱熱阻與其對流換熱熱阻的比值。因此在其他條件均相同的情況下,那塞特熱傳係數愈大表明發生於流體與固體壁面之間的對流換熱過愈為強烈。
基本介紹
- 中文名：那塞特熱傳係數
- 外文名：Nusselt number
- 套用領域：能源材料
- 別名：那塞特準則
- 作用：確定對流換熱
概念詳解
對流換熱傳遞能量時,要受傳導及物質傳遞兩方面的影響。除了液體金屬以外,一般流體的導熱係數都比較小,所以能量的傳遞主要依靠流體粒子的混亂運動。
如果流速及紊流的強度都較小,那那么巨觀的混合運動也弱,對能量的傳遞大為不利。當流速增加時,能促進低溫流體與高溫流體間的混合運動,這雖對單純的傳導機理不重要,但是,對能量傳遞卻很有利。因此,通過熱對流要傳遞某一定量的熱量時,低速區域要比高速區域需要較大的溫度梯度。
如果採用這些定性考察的結果,那么,可以粗略地描述由固體壁向形成素流的流體傳熱過程中產生的流體溫度分布。在貼近壁面處,由於流體粒子相對於邊界是靜止的,這時熱僅通過熱傳導傳遞。因此,這一層會產生較大的溫度梯度。再遠離壁面時,由於流體的混合運動有利於能量的傳遞,所以,此處的溫度梯度較緩和,在主流內則沒有溫度梯度。
如圖《溫度邊界層及等效傳導層》所示。通常把從壁面開始到無溫度梯度點的距離
稱為溫度邊界層的厚度( thermal-beunday layer),在此外側的流體溫度等於主流的溫度
。
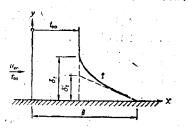
溫度邊界層及等效傳導層
如上所述，在界面處（y=0）因熱量只由傳導傳遞,所以由壁面向流體的傳熱量可由下式表示：
在已知溫度分布的情況下，可以利用這個傳熱量計算公式進行計算，但在工業上計算傳熱時用傳熱係數比較便利,所以為了不失掉其物理上的含義，有必要引進傳熱係數與界面處流體溫度梯度的關係。
下面取流體的代表溫度為主流溫度 時,來定義傳熱係數α,由對流換熱定律及壁面向流體的傳熱量計算公式聯立得：
引入指定換熱面系統形狀的特徵尺l，將上式改寫成無量綱形式,則可得
由上式可知，如果等效熱傳導層厚度
變小，則對流熱阻也變小，為了迅速傳遞更多的熱量,就必須把溫度邊界層的厚度儘量弄薄。為此，只要增加流速及使流動變成紊流狀態就可以了。若以表面隔熱為目的，則製造厚而靜止的邊界層是有利的。事實上，只要不引起混合運動，則有小空隙的隔熱材料由於空氣導熱係數小,對隔熱有利。
