邏輯斯諦映射

簡述

邏輯斯諦映射(logistic map)亦稱拋物線映射.表現複雜非線性行為的典型映射之一其具體形式為

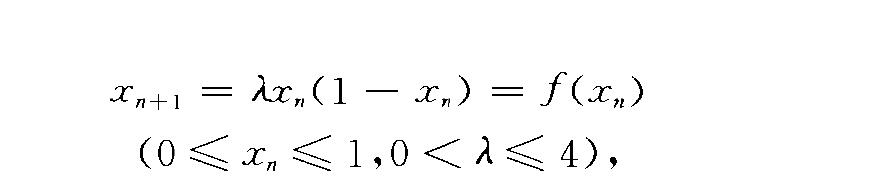
其中二，代表第n步狀態值.由於函式f(二。)是拋物線(見圖1)，由圖上可見二一1/2時，f(二。)達到最大值.1/4.拋物線映射疊代過程為:由任何初值二(、出發，按圖上箭頭進行，依次求出二，，二:，二3，…，在圖示例中就收斂到不動點二‘，即拋物線和直線y=二的交點.當參數幾變化時，系統演化形態可以多種多樣.當。G時，二，~Of 即二，一。是一個不動點. 當1G}1G3時，二。}1一 1八，它將可能收斂到圖上

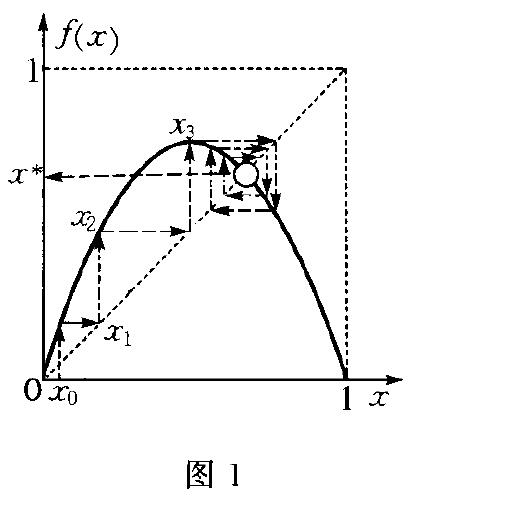
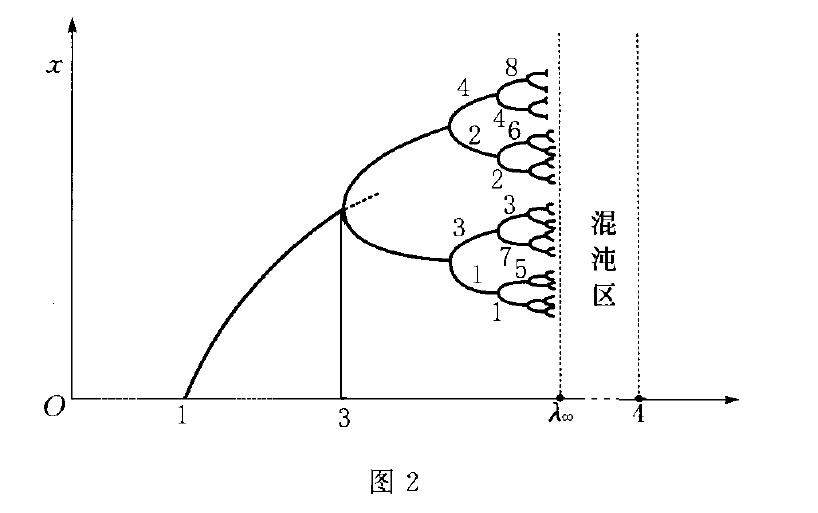
的另一個不動點二,..這些均為過去熟知之結果.但當參數.1} 3，可發現3G.1G3. 45時，二。在兩個值上來回跳動，稱為周期2解，它是映射二，十，=f(f}(二，)) 的不動點.幾繼續增大還有周期4、周期8等.直到幾_一3. 57"二，系統狀態為周期20'，即非周期態，這就是由倍周期而導致的混沌狀態(見圖2).

占倍

進而費根鮑姆((Feigenbaum,M. J.)還發現前面兩個相鄰分岔點之間的距離幾。一幾。一;逐漸接近於後面兩個相鄰分岔點之間距離},+ }一幾。的占倍，即

占稱為費根鮑姆常數.又發現周期2·狀態之間的距離d。趨近於周期2”十’狀態之間距離d,、的a倍，即

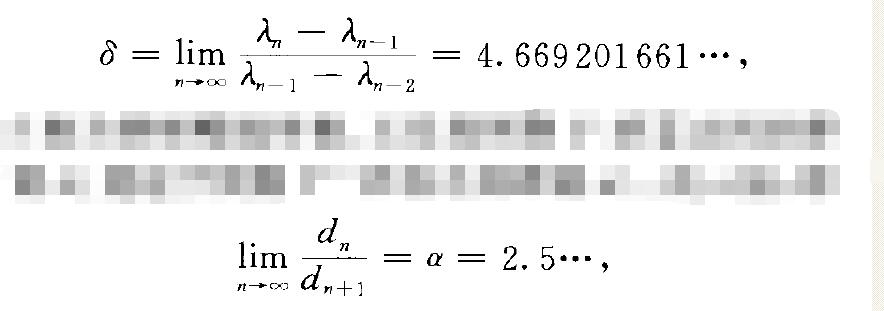
a也是無理數.