邏輯斯蒂增長曲線是一種由比利時數學家Verhulst首次發現的特殊曲線。後來,R.Pearl和L.J.Reed根據這一理論研究人口增長規則,因此,邏輯斯蒂增長的曲線也被稱為生長曲線或珍珠里德曲線。
基本介紹
- 中文名:邏輯斯諦增長
- 外文名:Logistic growth model
- 類型:數學模型
- 研究:植物群體的發病率
- 發現者:Verhulst
簡介
積分式
增長曲線模型概述
邏輯斯蒂生長曲線最小二乘法預測模式的建立
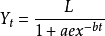
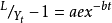
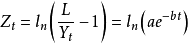
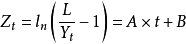
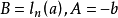
邏輯斯蒂增長曲線是一種由比利時數學家Verhulst首次發現的特殊曲線。後來,R.Pearl和L.J.Reed根據這一理論研究人口增長規則,因此,邏輯斯蒂增長的曲線也被稱為生長曲線或珍珠里德曲線。
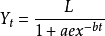
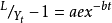
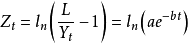
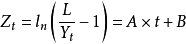
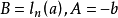
後來,R.Pearl和L.J.Reed根據這一理論研究人口增長規則,因此,邏輯斯蒂增長的曲線也被稱為生長曲線或珍珠里德曲線。 [1] 中文名 邏輯斯諦增長 外文名 Logistic ...
阻滯方程又叫阻滯方程,英文Logistic equation,是與密度有關的種群增長模型。目錄 1 邏輯斯諦方程簡介 2 時期 阻滯方程邏輯斯諦方程簡介 編輯 ...
指數式增長的不現實性,使學者提出了邏輯斯諦增長模型。 種群在有限環境下的邏輯斯諦增長模型 假定種群增長有一個環境所允許的最大種群值,稱為容納量,通常以K表示...
第三節 種群的指數增長 第四節 種群的邏輯斯諦增長 第五節 對種群增長模型的修正 第四章 種群間的相互關係 第一節 種群相互關係的類型 第二節 競爭 第三節...
洛特卡-沃爾泰拉競爭模型以邏輯斯諦增長為基礎。假定物種甲、乙單獨增長時,均按邏輯斯諦方程,即:對物種甲,對物種乙, 邏輯斯諦增長方程說明種群的增長率 dN/dt...
二十、種群在有限環境中的邏輯斯諦增長 二十一、種群增長模型的計算機模擬 二十二、種間關係模型的計算機模擬 二十三、齧齒動物的繁殖參數 二十四、齧齒動物巢區...
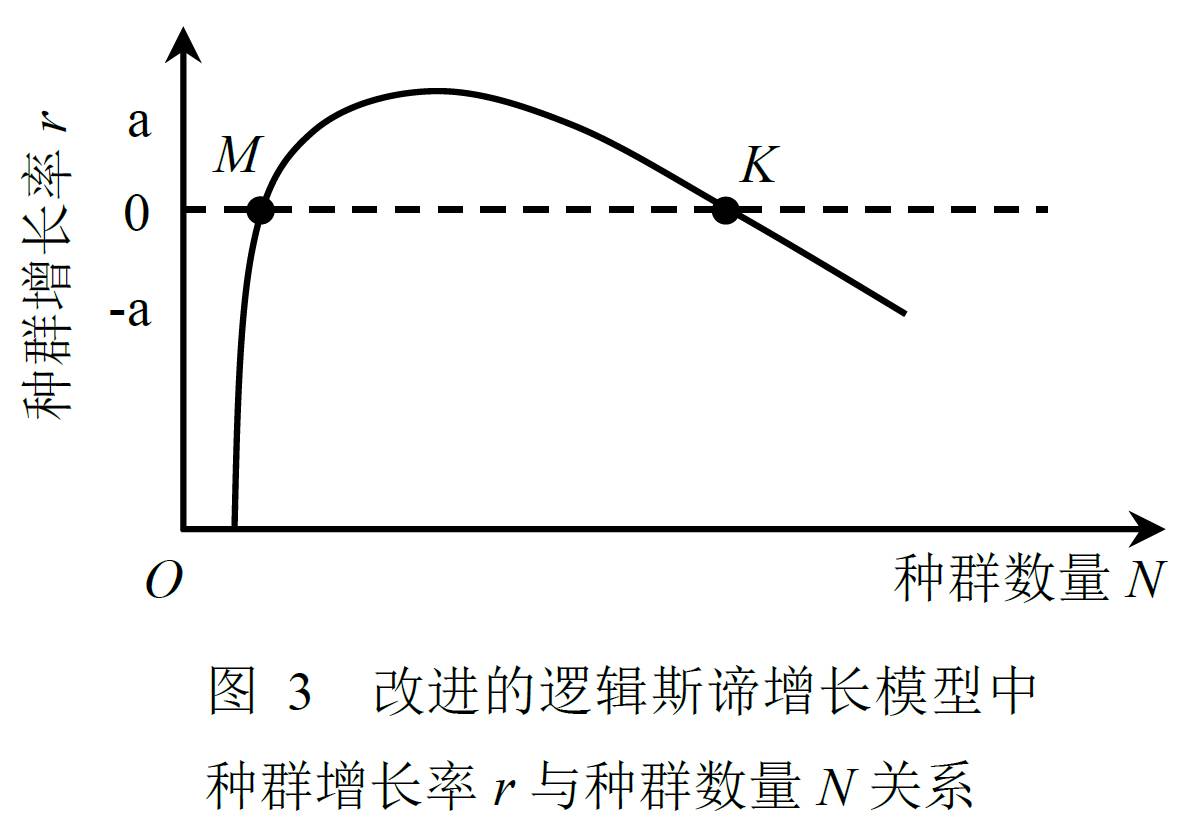
大多這樣的種群的個體數不斷地在其環境的負載能力上下波動,這種種群曲線成為S形,所以稱為S形曲線,這種增長方式稱為邏輯斯諦增長。 為了描述上述種群的數量增長過程...
環境氣候穩定,很少有難以預測的天災系統,生物密度很高,生物數量達到或接近環境容納量水平,即與種群邏輯斯諦增長模型的飽和K值相階級接近,稱為K選擇 ...
競爭和共存理論是邏輯斯諦增長模型的擴展野外研究表明競爭在自然界普遍存在植物競爭在富養生境和貧養生境有所不同通過利用共占資源或直接干擾而引起競爭競爭結果可能...
▪ 周限增長率 ▪ 幾何增長率 ▪ 指數增長 ▪ 邏輯斯諦增長 ▪ S型生長曲線 ▪ 平均擁擠度 ▪ 擁擠效應 ▪ 世代離散 ▪ 世代重疊 ▪ 種群...
在前一類環境中,動物種群數量達到或接近環境負載量水平,即與種群邏輯斯諦增長模型的飽和密度K接近,因此這種環境對生物的作用可稱為K 選擇。在後一類環境中,種群...
實驗一 種群在有限環境中的邏輯斯諦增長模擬 實驗實驗二 種群數量估計實驗三 種群生命表的編制與存活曲線實驗四 土壤動物種群的空間分布型測定...
實驗11種群在有限環境中的邏輯斯諦增長 實驗12種群空間分布格局的調查 第四章群落生態學 實驗13植物群落內生態因子的測定 實驗14校園內植物群落物種多樣性的調...
實驗9種群在有限環境中的邏輯斯諦增長實驗10生命表的編制實驗11種群內分布型的測定實驗12植物種群的種內競爭 更多詞條標籤: 出版物 , 書籍 ...
生態學》是2004年高等教育出版社出版的圖書,作者是里克萊夫斯 (Ricklefs Robert ...競爭和共存理論是邏輯斯諦增長模型的擴展野外研究表明競爭在自然界普遍存在...
種群生態學中的許多著名的原理和理論,如種群的邏輯斯諦增長模型、種間競爭排斥的高斯假說,都是在實驗種群的數學模型基礎上提出的。然而,必須指出的是,實驗室得出的...
