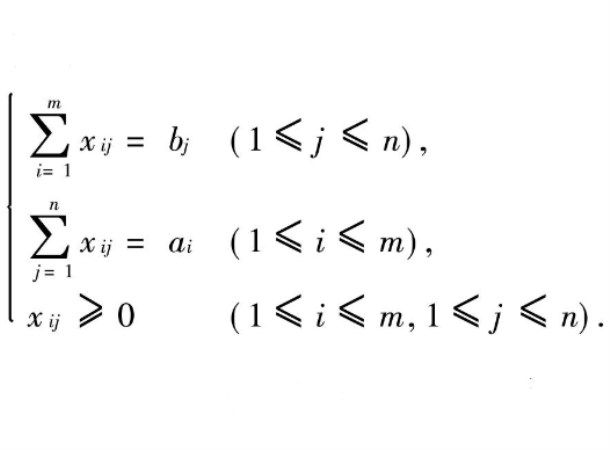運輸多面體

運輸多面體(transportation polytope)是一種與運輸問題關聯的多面體，若一個運輸多面體，它的所有頂點全是非退化，則它本身是非退化的；否則，就是退化的。

基本介紹

• 中文名：運輸多面體
• 外文名：transportation polytope
• 所屬學科：數學
• 所屬問題：組合學（組合多面形)
• 簡介：一種與運輸問題關聯的多面體

基本介紹

運輸多面體由如下方程和不等式組的解集所確定：對於給定兩個非負向量 和 ，

用 表示這個運輸多面體，它的階為m×n，若 的一個頂點，即mn維空間中的一個向量恰有 個非0分量，則稱它為非退化的，若一個運輸多面體，它的所有頂點全是非退化，則它本身是非退化的；否則，就是退化的。

相關介紹

如上所述，若 和 ，則這時被稱為中心運輸多面體，設 為 的一個頂點，記

兩個運輸多面體 和 ，，若對於頂點和頂點，有

則此兩頂點是等價的，若對每個的頂點都有的一個頂點與它等價，並且對的一個頂點也有的一個頂點與它等價，則和為等價運輸多面體。若a=b，則這時的稱為對稱運輸多面體，對於運輸多面體，若

其中，

則兩個運輸多面體和是等價多面體若且唯若對任何，均有

其中，signμ表示取值μ的符號，對於一個運輸多面體，若，則稱它為k退化運輸多面體，一個1退化運輸多面體使得，則稱它為退化的。