連鑄坯凝固傳熱數學模型是描述連鑄坯在連鑄機內凝固過程中熱傳遞導致鑄坯溫度分布的數學表達式。鑄坯凝固傳熱數學模型的適用性在於計算不同澆鑄條件下鑄坯溫度分布。
基本介紹
- 中文名：連鑄坯凝固傳熱數學模型
- 外文名：mathematicalmodel of heat transfer for solidification ofcontinuous casting slab or billet
- 學科：冶金工程
- 套用：計算不同澆鑄條件下鑄坯溫度分布
- 領域：連續鑄鋼
- 求解方法：解析法和數值法
研究意義,數學方程式,求解方法,數學模型驗證,套用,
研究意義
在連續鑄鋼過程中，鋼水澆入結晶器，形成規定形狀的固體坯殼，從結晶器鋼水彎月面開始鑄坯以一定的速度向下運動，經過二次噴水冷卻區和輻射冷卻區向切割設備移動，鑄坯在邊運行邊傳熱邊凝固的過程中，形成一個很長的液相穴（板坯連鑄時可達25～30m）。從中間罐澆入結晶器的注流動能引起液相穴內鋼水產生強制對流傳熱，熱連續地通過已凝固坯殼傳到外界使鑄坯完全凝固。其凝固速率決定於坯殼向外界傳熱的速率。而坯殼傳遞熱量的多少又決定於鋼種的熱物性、鑄坯經歷的不同冷卻區的邊界條件以及澆鑄工藝參數。
因此，可以根據鑄坯在結晶器、二冷區和輻射區所導出的熱量，來定量了解鑄坯在運動過程中凝固殼（厚度）的生長、鑄坯內的溫度分布以及液相穴的延伸長度即凝固終點等，這對於工藝參數的最佳化、鑄坯質量的改善和連鑄機設計等方面都具有十分重要的意義。因此，人們開發了連鑄坯凝固傳熱數學模型，並與計算機控制技術相結合，套用於連鑄生產並取得了顯著效果。
數學方程式
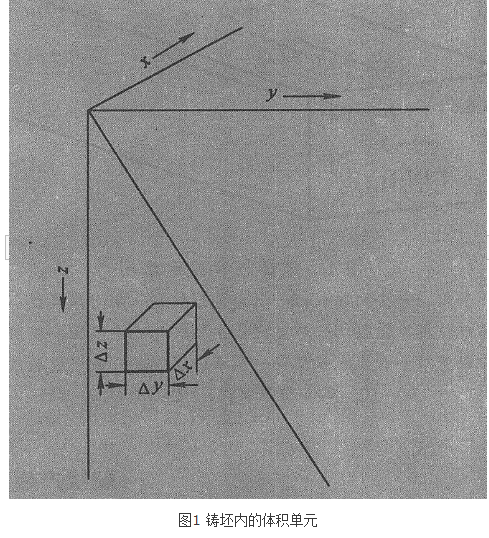
假想在凝固的鑄坯內取一個小的體積單元（圖1）它可以位於凝固殼內也可位於液相穴內，鑄坯以一定速度u向下運動。
為導出鑄坯凝固傳熱數學方程式，做以下5項假設：（1）忽略垂直方向（即拉坯方向）的傳熱（結晶器拉坯方向的導熱量僅占總熱量的3%～6%）。（2）澆注斷面呈對稱冷卻，即相對兩面的冷卻速率相同。（3）液相穴內僅靠傳導傳熱，忽略液體的對流傳熱。（4）鋼的熱物理常數如密度ρ、導熱係數λ和比定壓熱容Cp均不隨溫度而變化。（5）操作過程為穩定態。如拉速、鋼水溫度和結晶器鋼液面都是穩定的。根據建立數學模型的步驟，做體積單元體的熱平衡，即可得到以下偏微分方程：
沿結晶器液面的軸向位置z是與鑄坯拉速u和時間t有關的，即z=ut，把z值代入式（1）得：
式（2）是二維的熱傳導方程，用以描述方坯凝固過程的傳熱行為。
用上述熱傳導方程來預見鑄坯的溫度分布，必須確定鑄坯中體積單元從結晶器彎月面開始，以拉速u向下運動的初始條件，以及經過結晶器、二冷區和輻射區的鑄坯表面邊界條件。
（1）初始條件：規定在開始澆注時（t=0）結晶器彎月面鋼水溫度等於澆注溫度Tc。
t=0，0≤x≤a，0≤y≤b，T（x，y）=Tc（5）
（2）邊界條件：鑄坯內熱流是連續的。鑄坯表面的邊界條件在各冷卻區是不同的。
求解方法
求解偏微分方程的方法有解析法和數值法。解析法是對偏微分方程積分可得到精確解，但是由於連鑄過程的複雜性，需做許多假設（如鋼的導熱係數為常數等），求解極為煩雜，適用性也差。現在廣泛套用的是數值法求解，將偏微分方程化為差分方程，為此必須建立差分格線。
數學模型驗證
根據所建立的數學模型，模擬計算鑄坯的凝固過程，以決定影響凝固殼厚度，液相穴深度和表面溫度分布的工藝操作參數，這已成為連續鑄鋼鑄機設計、工藝分析和過程控制的重要手段。為驗證數學模型的計算結果，有以下6種方法：
（1）刺穿坯殼法。鑄坯出結晶器後，把凝固坯殼刺穿使液體鋼水流出來，然後測定凝固殼厚度與計算結果比較（也可用拉漏的鋼殼進行測定）。
（2）同位素示蹤法。在某一時刻隨注流加入放射性同位素（如Au）到結晶器內，注流的運動把同位素帶到液相穴深處，含有Au元素的鋼液凝固帶有放射性，而加入Au那一時刻已凝固的金屬不含放射性元素，這樣就可通過在不同位置上切取試片做自射線照相，分辨出凝固層厚度。
（3）打釘法。鑄坯出結晶器後，在二冷區的某一位置射入鋼釘，鋼釘的液相線溫度低於鋼種的液相線溫度，在液相區釘子完全熔化，在兩相區則部分熔化，而在固相區釘子未熔化，這樣取出試片就可直接分辨出凝固層厚度。
（4）測定板坯鼓肚以決定液相穴的位置。在接近矯直點前某一位置，把支承輥的開口度適當放大，如鑄坯內還有液相，就會有鼓肚。用此法可以粗略估計液相穴長度。
（5）從結晶器上方放入密度大、包有放射性元素的球（如鎢球），此球以相當大的速度下降到液相穴底部，然後用蓋格計數器測定出放射性時在鑄坯內的位置，以確定液相穴長度。
（6）測定鑄坯表面溫度。在二冷區的不同冷卻段直到拉矯輥處，選擇幾個測溫點，用高溫計測定不同時刻鑄坯的表面溫度，得到Ts—t曲線，並與模型計算的表面溫度分布對比。
套用
連鑄坯凝固傳熱數學模型的適用性在於計算不同澆鑄條件下鑄坯溫度分布。主要用於以下三方面：
（1）連鑄工藝操作參數的最佳化。利用數學模型，可分別計算澆注工藝參數（如澆注溫度、拉速、冷卻水量等）對凝固殼厚度、液相穴長度和表面溫度的影響，以得出滿足鑄機產量和鑄坯質量要求的合理操作參數。如提高拉速，就會減少鋼水在結晶器的停留時間，導致出結晶器坯殼厚度變薄，增加了拉漏的危險性。為此，使用數學模型可以計算不同拉速和不同結晶器長度與出結晶器坯殼厚度的關係。經常使用的結晶器有效工作長度為625mm，出結晶器坯殼厚度：板坯約20mm，小方坯約10mm才能保證不拉漏。因此，增加拉速，需保持鑄坯出結晶器時坯殼厚度不變，為此必須適當增加結晶器長度，以保持鋼水在結晶器內停留時間不變。
（2）二次噴水冷卻的合理設計。曾經發現，鑄坯中間裂紋是鑄坯表面傳熱速率突然減少使表面回熱所致。這種現象可能是在二冷區的兩個冷卻段，或是在同一冷卻段噴嘴不良使冷卻不均勻造成的。表面回熱是產生中間裂紋的驅動力。顯然，要防止中間裂紋的產生，就必須儘可能的把鑄坯表面回熱減到最小。在生產上就是改進噴水冷卻條件，把鑄坯回熱與噴水條件（如噴水壓力、噴射距離）聯繫起來。為此，使用數學模型就可計算為避免產生中間裂紋，在二冷區鑄坯所要求的熱流分布，然後轉換為傳熱係數分布。根據傳熱係數與噴水水流密度的關係式，得到二冷區合理的水量分布，以選擇合適的噴嘴和噴水參數。
（3）連鑄機的最佳化設計。在設計連鑄機時，根據實際條件和產品要求，在數學模型的計算程式中輸入工藝參數，設計多種方案，以選擇滿足鑄機生產率和產品質量的最佳方案。
