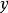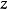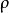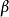連續混沌系統背景
混沌學是80年代初期建立起來的一門新興學科。它是以一種新的方式重新對自然進行描述,揭示了自然界及人類社會的複雜性、有序和無序的統一,大大加深了人們對自然界的了解。目前,混沌的研究不僅遍及自然科學的各個領域,而且已有成功的實際套用。
近年來,基於觀察時間序列的混沌控制理論和實驗驗證研究逐漸成熟起來,這些方法的共同特點是對被控混沌系統的先驗知識要求較少。這些方法包括:一是基於時間序列辨識模型和Lyapunov法來設計非線性反饋控制器的方法,如Poznyak等人用動態神經網路、Chen等人用二階Volterra級數辨識模型實現了未知連續混沌系統的有效控制,但它要求較大的存儲空間存儲觀察時間序列,以便用於離線方式進行時間序列模型辨識;二是用觀察數據來脈動地改變混沌系統的狀態變數的脈衝控制法,該方法通過對混沌系統輸出的連續觀察來構造控制輸入信號,需要在一個很短的時間內改變狀態變數,然而並不是所有混沌系統都能通過直接改變系統狀態變數就能實現混沌現象的控制;三是羅曉曙等人採用的有限脈衝回響濾波器控制混沌方法,但這種方法的控制參數選擇較困難。
連續混沌系統數學模型
連續混沌動力學系統:
常用連續混沌系統
Lorenz 系統
Lorenz 系統最初是 Edward Lorenz 研究的普通微分方程組。 對某些參數值和初始條件有混沌的解決方案是值得注意的。 特別地,Lorenz 吸引子是 Lorenz 系統的一套混沌解決方案,當繪製時,它類似於蝴蝶,如圖1。
 圖1Lorenz系統( ρ = 28, σ = 10, and β = 8/3)
圖1Lorenz系統( ρ = 28, σ = 10, and β = 8/3)1963年,愛德華·洛倫茲(Edward Lorenz)開發了一個簡化的大氣對流數學模型。該模型是現在稱為洛倫茲方程的三個常微分方程的系統:
其中,
、
和
構成系統狀態,
是時間,
、
和
是系統參數。Lorenz方程也出現在雷射器的簡化模型中,
發電機,
無刷直流電機,電路,化學反應和正向滲透。
從技術的角度來看,Lorenz系統是
非線性的、非周期的、三維的和確定性的。
Chua’s 系統
Chua’s系統是一種電路系統,自從提出以來,由於其巨大的套用前景,近年來已成為非線性電路中混沌控制及神經網路研究的新熱點。Chua’s電路可以展現任何三階非線性系統的定量動力學狀態,其中包括一個奇對稱的三部分分段線性函式。系統的狀態方程為:
式中,非線性項
,當系統取
,
,
,
時,上式描述的系統呈混沌狀態。
 圖2 Chua’s 系統的平面渦旋吸引子
圖2 Chua’s 系統的平面渦旋吸引子混沌同步
混沌同步即一個系統的軌道將收斂於另一系統軌道的同一值,它們之間始終保持步調一致,且這種同步是步調穩定的。
驅動回響同步
驅動回響同步使用驅動變數替換回響系統中的變數,也可稱為變數替換型。在驅動回響同步中必須把一個混沌系統(驅動系統)分成兩個子系統:一是穩定的子系統(李亞普諾夫指數均為負值),二是不穩定的子系統,這大大限制了該類型的實際套用範圍。文獻 提出了一種改進方案,稱為主動被動同步法。它將原系統寫成含有某種驅動變數的非自治系統形式,複製相同的回響系統,通過用線性化穩定性分析方法或李亞普諾夫函式方法分析兩個系統的差值,證明它們達到了穩定同步。這種方法可以實現兩個混沌系統的同步。
反饋同步
考慮非線性混沌系統的輸出信號與輸入信號之間的自反饋耦合,或者從系統外部強迫輸入一定的周期信號,或者直接把系統本身的輸出信號取出一部分但經過時間延時後再反饋到混沌系統中去,作為控制信號,通過調節控制信號的大小和權重因子,達到穩定所期望的周期信號。Pyragas提出的連續變數反饋混沌控制方案分為兩個步驟:先記錄所需的混沌信號,保存下來;再利用小的反饋微擾信號作為控制信號,反饋到原系統中去。適當的調整反饋微擾信號的權重因子可以實現混沌同步。該方法不僅可以套用於一個變數,也可拓廣於多個變數。文獻 對變數反饋法進行了詳細的仿真和穩定性分析,當三個反饋變數相等,即可同步,且越大,同步效果越佳。如果用單變數反饋,最大李雅普諾夫指數隨增益係數的變化有個最小值,對應最佳同步。
適應方法控制同步
1994年John和Amritkar給出了一種採用自適應控制實現混沌同步的方法,對可得到的系統參數進行控制,使系統的所有變數可自由演化。受控參數的變化依賴於兩個因素:一為系統輸出變數與期望軌道的相應變數之差;二是受控參數的值與期望軌道相應的參數值之間的差別。運用自適應方法Lorenz和Rossler系統可達到同步,也可實現高階混沌系統和超混沌系統的同步,超混沌系統與混沌系統的不同之處在於存在兩個正的李亞普諾夫指數,實現超混沌同步控制並不一定要求組合系統的條件指數必須小於零;在都能實現同步控制的控制參數下,控制能量越大,同步暫態過程越短。在相同的控制能量下,混沌系統較之超混沌系統更易於控制。
神經網路同步控制方法
人工神經網路(簡稱ANN)是由大量基本單元(神經元)按一定結構連線而成的複雜非線性系統。自從神經網路的第一個模型建立以來,ANN的研究幾經興衰,其中兩項理論成果的提出對ANN的研究起到了直接的推動作用,其一是Hopfield關於動態神經網路及其穩定性的研究,其二是用於多層感知器網路的學習算法反向傳播(BP)算法。徑向基函式神經網路因其具有快速的學習速度,同時和BP算法一樣,能以任意精度逼近任意連續函式,可用神經網路逼近原系統和待同步系統,並以兩個網路的輸出之差作為待同步系統的控制信號。


 圖1Lorenz系統( ρ = 28, σ = 10, and β = 8/3)
圖1Lorenz系統( ρ = 28, σ = 10, and β = 8/3)


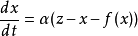



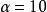

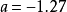

 圖2 Chua’s 系統的平面渦旋吸引子
圖2 Chua’s 系統的平面渦旋吸引子