逆波蘭表達式又叫做後綴表達式。逆波蘭表示法是波蘭邏輯學家J・盧卡西維茲(J・ Lukasewicz)於1929年首先提出的一種表達式的表示方法。後來,人們就把用這種表示法寫出的表達式稱作“逆波蘭表達式”。逆波蘭表達式把運算量寫在前面,把算符寫在後面。
基本介紹
- 中文名:逆波蘭表達式
- 外文名:Reverse Polish Notation
- 別名:後綴表達式
- 提出者:盧卡西維茲
- 時間:1929年
- 套用領域:數理科學
定義
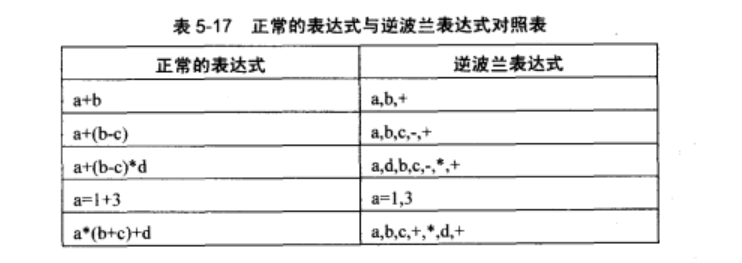
算法步驟
算法框圖
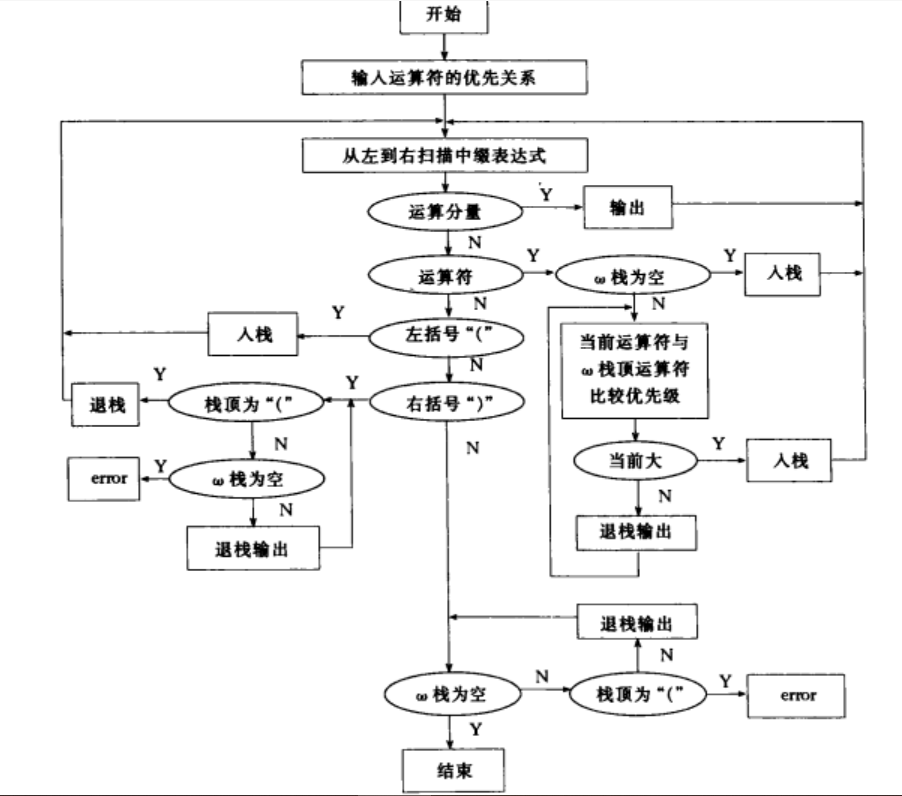
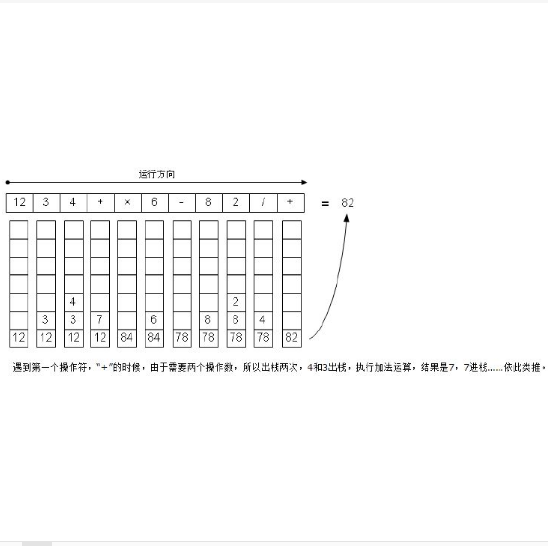
逆波蘭表達式又叫做後綴表達式。逆波蘭表示法是波蘭邏輯學家J・盧卡西維茲(J・ Lukasewicz)於1929年首先提出的一種表達式的表示方法。後來,人們就把用這種表示法寫出的表達式稱作“逆波蘭表達式”。逆波蘭表達式把運算量寫在前面,把算符寫在後面。


逆波蘭表達式又叫做後綴表達式。逆波蘭表示法是波蘭邏輯學家J・盧卡西維茲(J・ Lukasewicz)於1929年首先提出的一種表達式的表示方法。後來,人們就把用這種表示法...
介紹逆波蘭表達式(Reverse Polish Notation),簡稱為RPN,由J. Lukasiewicz(12/21/1878 – 02/13/1956)發展而來,在避免使用括弧的情況下,完成表達式的有優先權的...
逆波蘭式(Reverse Polish notation,RPN,或逆波蘭記法),也叫後綴表達式(將運算符寫在運算元之後)...
2 逆波蘭表達式--RPN ▪ 逆波蘭表達式簡介 ▪ 逆波蘭表達式實例 3 相對位移--RPN RPN風險係數--RPN 編輯 推薦出負責的方案以及完成日期,這些推薦方案...
中間語言逆波蘭表示 逆波蘭表示又稱後綴表示法,它是最簡單的一種中間代碼表示形式,早在編譯程式出現之前,它就用於表示算術表達式。...
2.2.2 逆波蘭表達式 1252.2.3 Shunting-yard算法 1262.2.4 標籤與跳轉 1302.2.5 條件語句 1352.2.6 子程式調用 1372.2.7 變數 138...
概述JSEL是一個基於逆波蘭式結構,採用JS運算規則的簡單的表達式解釋引擎。 同時它還是一個JSON解析引擎。基本特徵* 基於逆波蘭式這個簡單的計算模型,最大的特點就是...
4.2.3 逆波蘭表達式4.2.4 檢索指令表的生成4.2.5 檢索實施4.3 其他檢索方法4.3.1 布爾檢索4.3.2 後綴樹和後綴數組4.3.3 加權檢索...
計算是在CDEF部分中指定的,使用逆波蘭表達式( RPN )表示的。我們要求RRDtool所作的事情是:`取數據源myspeed, 以及數值1000;把他們相乘` 。在此不要被RPN表達式...
5.2 表達式的逆波蘭式及其語法制導生成5.3 表達式的三元式和樹及其語法制導生成5.4 表達式四元式及其語法制導生成5.5 類型檢查與類型轉換5.6 語句的中間代碼及其...
5.2.3 逆波蘭表達式1185.2.4 檢索指令表的生成1205.2.5 檢索實施1215.3 後綴數組索引1225.3.1 後綴樹概念1225.3.2 後綴樹原理122...
5.2.3 逆波蘭表達式5.2.4 檢索指令表的生成5.2.5 檢索實施5.3 布爾檢索5.4 加權檢索5.4.1 檢索詞加權檢索5.4.2 詞頻加權檢索...
5.2.3 逆波蘭表達式1185.2.4 檢索指令表的生成1205.2.5 檢索實施1215.3 後綴數組索引1225.3.1 後綴樹概念1225.3.2 後綴樹原理122...
10.1 逆波蘭式計算器 169 10.1.1 計算rpn表達式 169 10.1.2 寫一個rpn函式 170 10.1.3 添加更多的操作符 172 10.2 從希思羅機場到倫敦 173 10.2.1...
