逆位似點(inverse homothetic points)是與兩圓位似點相關的一對點,指一個圓與兩已知圓分別相切於A和A′,S為兩已知圓的位似中心,若直線AA′通過S,且A,A′不是對於S的位似點,則A和A′稱為兩已知圓的位似中心的逆位似點。
基本介紹
- 中文名:逆位似點
- 外文名:inverse homothetic points
- 所屬學科:數學
- 所屬問題:平面幾何(比例與相似形)
- 簡介:與兩圓位似點相關的一對點
基本介紹
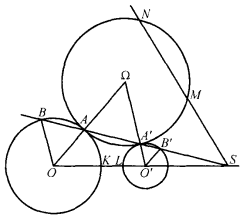

逆位似點的性質



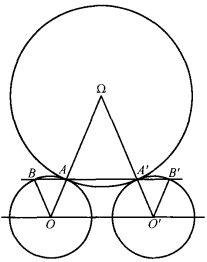

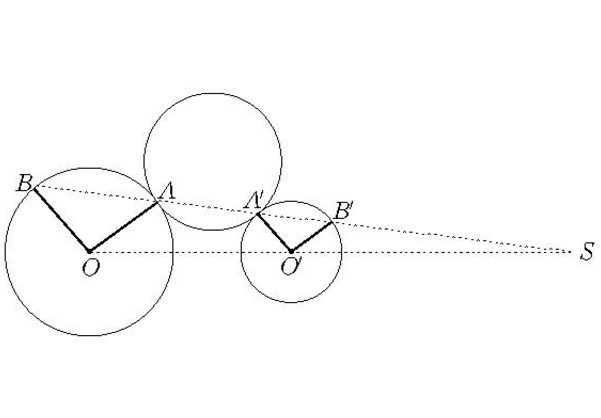
逆位似點(inverse homothetic points)是與兩圓位似點相關的一對點,指一個圓與兩已知圓分別相切於A和A′,S為兩已知圓的位似中心,若直線AA′通過S,且A,A′不是對於S的位似點,則A和A′稱為兩已知圓的位似中心的逆位似點。







逆位似點(inverse homothetic points)是與兩圓位似點相關的一對點,指一個圓與兩已知圓分別相切於A和A′,S為兩已知圓的位似中心,若直線AA′通過S,且A,A′不是對於S的位似點,則A和A′稱為兩已...
當任一雙對應點A,A′在點O的兩側,這時圖形F和F′稱為逆位似,或稱圖形F和F′內位似,點O稱為內位似中心,或內相似中心。這時規定位似比k 幾何變換 幾何變換是把一個幾何圖形按照某種法則或規律變成另一種圖形的過程。因為幾何圖形都是點的集合,所以幾何變換都是通過點的變換實現的。例如,在平面幾何中,...
逆位的星幣三,教堂垮台了,可能是不願合作、破局,大家均有不同的理念,或是建造的技藝不足,能力差,技能差,沒有具備升任任務所需的知識,無法為他人所肯定;關係出現裂痕,雙方對於未來沒有共識沒有想法,只做自己的事情對他人不聞不問。在逆位的星幣三上面,則代表著自己雖然知道自己的問題點在哪裡,也明白...
逆位釋義 逆位的權杖國王,管理能力不佳,權力使用的不對,不會帶人,所帶領的團理無法前進,或是濫用權力,使的權杖是一根打人的棒子,用自己的權力地位來修理部下,不顧下屬他人的意見,也有可能是提議無法獲得上級的支持,所做的事情不被肯定。逆位的權杖國王代表著自己沒有足夠的能力去改善目前的情況,卻還去找尋...
逆位釋義 逆位的權杖十,倒下了,權杖散落一地,已經過勞不堪,無法再承受更多,失去原本勉強的平衡倒地不起,也有可能是團體解體了,解散了。在逆位的權杖十上來看,也是自己因為太過的高估自己的能力,而有一些無法負擔的狀況發生,但是比正位的權杖十要來的輕微許多了,因為逆位的權杖十有自己懂得在一些困境中找出...
逆位釋義 逆位的權杖三要注意的是可能貿易不如預期,海在上方代表波動變大,有事先未能預測出的風險存在,對行動力存在影響,可能行程有所延遲,有所耽擱,遲疑不前等等,而領導人物的消失可能是沒有夠力的領導核心人物,或是上層決策錯誤,決定不對,無法凝聚向心力,造成人際關係之間的分離分裂,團隊協力合作的部分...
但棘鮃科種類也有眼睛逆位的標本報導。為什麼哪隻眼睛移動的性狀進化到棘鮃科魚類就相對固定下來了呢?哪隻眼睛移動與上方雙視野範圍大小是無關的,那可能是什麼原因造成的呢?是否有可能是已經營底棲生活的種類,其種內個體之間交配的配偶選擇,在某種程度上是否與眼睛分布位置有關?如眼睛位於右側的雄性個體,是否更...
塔羅主位牌—女祭司逆位。詭秘、猜疑、冷淡、逞強、矜持、孤獨……處女座星語—之所以自私,只因為無私。不忍傷害任何她所在乎的人,所以習慣隱忍、隱藏自我,自傷至極也無所謂……楠竹曰:那是一個在乎的極限,是一個類似海平線的高度,是一個他生命中人事物的沉浮點,是他即使追求刺激也能回復平靜的心湖。然,...
塔羅主位牌——女祭司逆位。詭秘、猜疑、冷淡、逞強、矜持、孤獨……處女座星語——之所以自私,只因為無私。不忍傷害任何她所在乎的人,所以習慣隱忍、隱藏自我,自傷至極也無所謂……楠竹曰:那是一個在乎的極限,是一個類似海平線的高度,是一個他生命中人事物的沉浮點,是他即使追求刺激也能回復平靜的心湖。
