迴轉拋物面

迴轉拋物面(paraboloid surface of revolution)是一種曲線迴轉面，以拋物線為母線，繞它本身的軸迴轉而成的曲線迴轉面稱為迴轉拋物面。

基本介紹

• 中文名：迴轉拋物面
• 外文名：paraboloid surface of revolution
• 所屬學科：數學
• 所屬問題：解析幾何
• 相關概念：迴轉二次曲面、母線等

基本介紹

迴轉拋物面(paraboloid surface of revolution)是一種曲線迴轉面，以拋物線為母線，繞它本身的軸迴轉而成的曲線迴轉面稱為迴轉拋物面，如圖1所示，其投影圖如圖2所示，V面投影的輪廓線就是拋物線本身，而H面投影的輪廓線是圓。

圖1

圖2

迴轉面

迴轉面是由一條曲線繞一條固定直線在空間轉動一周所產生的曲面，又稱旋轉面。曲線Γ叫做迴轉面的母線，直線叫做迴轉面的迴轉軸。取迴轉軸為Z軸，母線為

的迴轉面方程是

例如，以曲線

為母線，Z軸為迴轉軸的迴轉面方程是

當母線是平面曲線，且軸在這曲線所在的平面上時，以軸為界的半平面叫做經平面，它與曲面的交線叫做經線(子午線)；與軸垂直的平面叫做緯平面，它與曲面的交線叫做緯線 (平行圈)。旋轉曲面的所有經線都相同，而緯線則是以軸為聯心線的一組圓。

迴轉形式的二次曲面

如圖3所示，以OZ為旋轉軸，在V面中選取曲面的母線。則在圖3 (a)中，曲面的母線為兩平行於OZ軸的直線，其方程為

在圖3(b) 中，曲面的母線為兩相交直線，OZ軸平分這兩直線所夾之角，曲面母線的方程為

在圖3(c)中，曲面的母線為一橢圓(或圓)，其方程為

在圖3(d) 中，曲面的母線為一拋物線，其方程為

在圖3(e) 中，有三種曲面的母線，其中兩種為雙曲線，另一種是它們的漸近線。這三種曲面母線的方程分別為

圖3

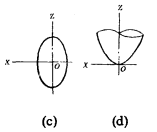
圖3

圖3（e）

可得上述幾種母線所形成的迴轉面的方程依次為：

(1) 圓柱面：

(2) 圓錐面：

(3)迴轉橢球面：

(4)拋物迴轉面：

(5)單葉雙曲迴轉面：

(6)雙葉雙曲面迴轉面：

應當注意，當a=c時，迴轉橢球面就變為球面了。

可以證明，在圖3 (e) 中，經過圓錐面錐頂的截平面與圓錐面的截交線——直線正是該截平面與其它兩種曲面的截交線的漸近線。

上述六種曲面概括了所有迴轉形式的二次曲面，也就是說，任意一個迴轉形式的二次曲面一定為上述六種曲面中的一種。