近點幅角

近點幅角（ω）也做近心點幅角。是描述在軌道上天體在近拱點（最靠近中心的點）時，相對於升交點（由南向北經過參考平面的點）的角度，也是軌道要素之一。這個角度是在軌道平面上量度的，方向則是天體運動的方向（在特定的軌道型式中會換用特定的名詞，像日心軌道是"近日點角"，地心軌道是"近地點角"，一般稱為"近點幅角"或"近拱點角"）。近點幅角為0度的意義是當天體最靠近中心點時也同時由南向北的通過參考平面；近點幅角為90度的意義則是當天體最靠近中心點時，位於參考平面的最北方。將近點幅角加上升交點經度就得到近心點經度。

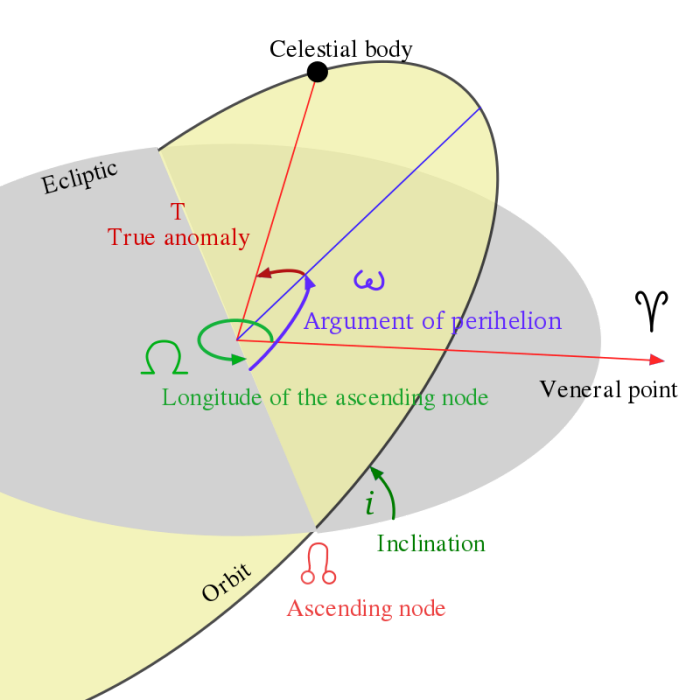
基本介紹

• 中文名：近點幅角
• 外文名：argument of perigee

在太空動力學，近心點幅角{\displaystyle \omega \,}可由下式計算：

• {\displaystyle \omega =\arccos {{\mathbf {n} \cdot \mathbf {e} } \over {\mathbf {\left|n\right|} \mathbf {\left|e\right|} }}}
  
• （如果{\displaystyle e_{z}<0\,}，那么{\displaystyle \omega =2\pi -\omega \,}）
  

此處：

• {\displaystyle \mathbf {n} }是指向昇交點的向量（此處是z-分量{\displaystyle \mathbf {n} }為0），
  
• {\displaystyle \mathbf {e} }是離心向量（指向近心點的方向）。
  

在赤道軌道上，無須精確的定義此一參數，他經常被假設如下：

• {\displaystyle \omega =\arccos {{e_{x}} \over {\mathbf {\left|e\right|} }}}
  

此處：

• {\displaystyle e_{x}\,}是離心向量的x-分量{\displaystyle \mathbf {e} \,}
  

在原軌道的情況下，經常會假設近心點就在昇交點的方向下，也就是{\displaystyle \omega =0\,}。