水輪機及水泵等水力機械的實現能量轉換部件中的水流運動。
基本介紹
- 中文名:轉輪中的水流運動
- 外文名:Motionof flow in runner
- 其他名稱:葉輪機中的水流運動
概念,運動機理及計算,
概念
水輪機及水泵等水力機械的實現能量轉換部件中的水流運動。
運動機理及計算
L.歐拉在1754年提出葉輪機的基本方程式,奠定了一切轉輪式動力機械的理論基礎。
轉輪是水流實現能量轉換的部件,其上具有形狀扭曲的葉片,水流從葉片之間通道中流過。在水輪機中,水流流過轉輪時對葉片做功,使轉輪轉動,把水流的能量轉換為機械能。對於水泵,則是由電動機帶動水泵的轉輪轉動,葉片把機械能傳遞給流過其中的水流,從而使水體的能量增加。轉輪內水流運動與轉輪的類型密切相關。
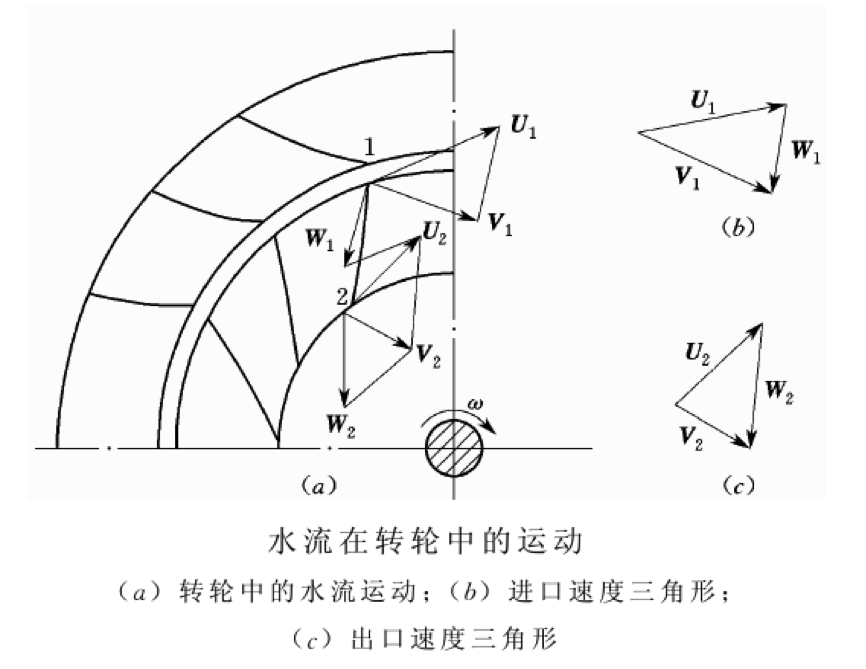
圖(a)示出了水輪機中的水流情況,水流從活動導葉流出後,從轉輪外緣流入,通過葉片間流道,從轉輪中心處流出。因此,水流相對轉輪有一運動。同時,當水輪機轉動時,它們還隨轉輪一起轉動。若在地球上建立定坐標系,把動坐標系設在轉輪上,那么,水流質點相對於轉輪葉片的流動就是相對運動,用W表示其速度。葉片之間某處的水流質點所具有的相對速度可認為與該處葉片表面相切。水流質點和轉輪一起相對於地球做的等速旋轉運動,就是牽連運動。它的方向是圓周的切線方向,用U表示。水流質點相對於地球的運動就是絕對運動,其速度稱為絕對速度,用V表示。絕對速度V等於相對速度W和牽連速度U的矢量和,即V=W+U。
在圖(a)中,水流在轉輪外緣1點處以絕對速度V流入,由於水流對葉片的作用,使轉輪以角速度(ω)旋轉。因此,絕對速度(V1)可以分解為圓周切向速度(U1)和沿葉片該處切線方向的相對速度(W1),由矢量求
和的作圖方法可以得到由V1,、W1,、U1,組成的轉輪進口速度三角形見圖(b)。水流從轉輪內緣的2點處流出,在這裡相對速度為W2,圓周切向速度為U2,合成出口處的絕對速度(V2)。由W2,、U2及V2組成轉輪出口的速度三角形,見圖(c)。流經轉輪的水流在不同的運動空間位置上都可做出這樣一個速度三角形。
對於水泵,水流情況正好相反。水流從葉輪中心流入,而從叫輪外緣流出,因此具有相對速度(W)。當水流進入葉輪後,都隨之轉動,就具有牽連速度(U),它們合成後就是水流質點相對於定坐標系的絕對速度(V)。對於水泵葉輪中任一運動空間位置也可做出速度三角形。無論是水輪機還是水泵,只有當假設葉片數目趨於無限多,每個葉片趨於無限薄時,才能認為相對速度是沿該處葉片表面的切線方向。若葉片數目是有限的,葉片之間的流道中就會出現旋渦和速度分布的不均勻,就要對由上述假定得出的公式加以修正。葉輪中的相對運動由試驗表明其隨時間變化不大,可以近似地認為是恆定流動,而絕對運動是非恆定流動。
大量試驗表明:在流動不脫體的情況下,水流的黏性影響主要表現在緊挨固體邊壁的一層很薄的水層——邊界層里,而在邊界層以外,可忽略黏性影響,作為理想流體的流動處理。只是在對葉輪中的水力損失或阻力進行研究計算時,才套用有關邊界層理論考慮黏性的影響。由於對水流作了理想流體的假定,在進行水力計算時,就可套用理想流體運動規律的歐拉運動微分方程式。