介紹
軌道子空間(orbital subspace)張量對稱類Vx(G)的子空間.設{e},ez,...}e,}}為V的基,aE1'
} .,} ,V x ( G)的子空間<e a=T (G, X)孺}aEG)稱為Vx(G)對應於a的軌道子空間.弗里斯(Freese,R. )首先證明了軌道子空間的維數為

張量對稱類Vx(G)可分解為軌道子空間的直和.由eaa並。若且唯若aE,}}所以Vs(G)可表示為
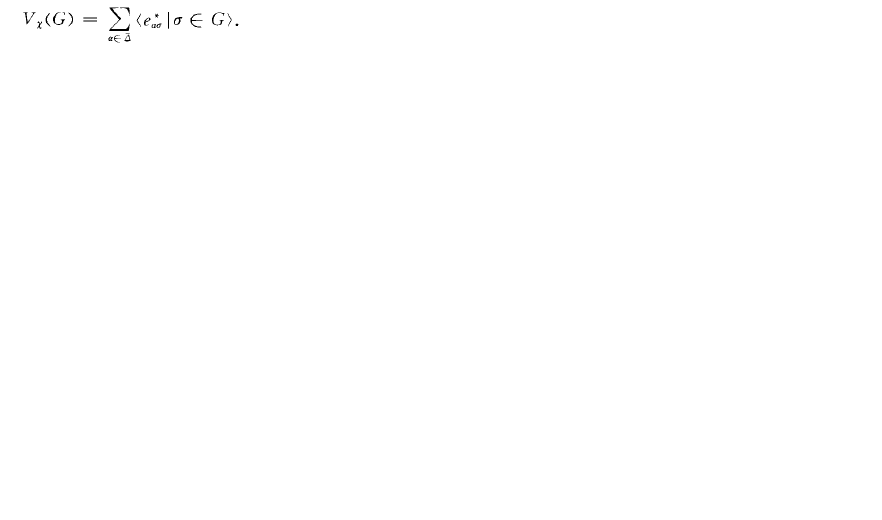
對於a任乙可以選取s。個序列amaz,...,as,使{e城,eQz ,...,eaQ}組成軌道子空間((eaa }aEG)的基·設乃按字典次序排列為乃一{a,R,y,...},對R,y等也類似地分別選出、,個與、,個序列,這樣就組成一個重要的集合記為乙一{ai } az,一a=o;R
RZ,...,R,};y
y
.. , y,Y ;…}.於是,{‘}。任乙}就構成張量對稱類Vx(G)的基.
