赫茲公式（Hertz Formula），也稱為赫茲方程，是德國物理學家海因里希·魯道夫·赫茲（Heinrich Rudolf Hertz）於1882年所發表論文中所提出的有關彈性體接觸的理論公式。其主要是研究疲勞、摩擦以及任何有接觸體之間相互作用的基本方程。
基本介紹
- 中文名：赫茲公式
- 外文名：Hertz Formula,Hertz equation
- 領域：彈性力學
- 用途：接觸應力計算
- 提出者：Heinrich Rudolf Hertz
- 時間：1882年
- 別稱：赫茲方程
提出,介紹,
提出
赫茲1882年發表了關於接觸力學的著名文章“關於彈性固體的接觸（On the contact of elastic solids）”，赫茲進行這方面研究的初衷是為了理解外力如何導致材料光學性質的改變。
Heinrich Rudolf Hertz
Heinrich Rudolf Hertz為了發展他的理論，赫茲用一個玻璃球放置在一個稜鏡上，他首先觀察到這個系統形成了橢圓形的牛頓環，以此實驗觀察，赫茲假設玻璃球對稜鏡施加的壓力也為橢圓分布。隨後他根據壓力分布計算了玻璃球導致的稜鏡的位移並反算出牛頓環，以此再和實驗觀察對比以檢驗理論的正確性。最後赫茲得到了接觸應力和法向載入力，接觸體的曲率半徑，以及彈性模量之間的關係。赫茲的方程是研究疲勞，摩擦以及任何有接觸體之間相互作用的基本方程。
介紹
兩圓柱體接觸由於直齒輪在節點附近往往是單對齒嚙合區，輪齒受力較大，故點蝕首先出現於節點附近。因此，通常計算節點的接觸疲勞強度。如圖表示一對漸開線直齒圓柱齒輪在節點接觸的情況。為了簡化計算，用一對軸線平行的圓柱體代替它，兩圓柱的半徑ρ1、ρ2分別等於兩齒廓在節點處的曲率半徑。由彈性力學可知，當一對軸線平行的圓柱體相接觸並受壓力作用時，將由線接觸變為面接觸，其接觸面為一狹長矩形，在接觸面上產生接觸應力，並且最大接觸應力位於接觸區中線上，其數值為
式中
：接觸應力（Mpa）
L：接觸線長度（mm）
±：正號用於外接觸，負號用於內接觸
上式表明接觸應力應隨齒廓上各接觸點的綜合曲率半徑的變化而不同，且靠近節點的齒根處最大。但為了簡化計算，通常控制節點處的接觸應力。
兩圓柱體接觸時，接觸面半寬a為：
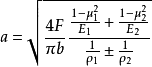
兩球體接觸時，接觸面半徑c為：
