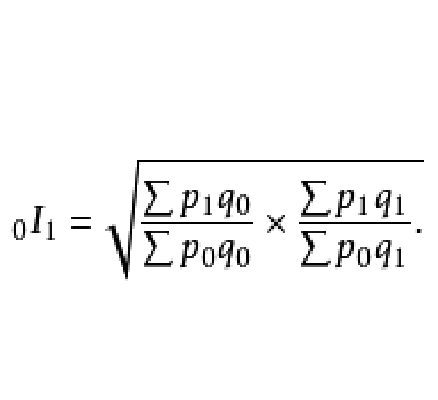費希爾理想公式

費希爾理想公式(Fisher′s formula)是美國著名統計學家J.費希爾於1927年在其名著《統計指數的編制》中提出的主張：取拉斯貝爾斯指數和派許指數的幾何平均數的一種物價指數公式。費希爾認為此公式既能滿足時間顛倒測驗，又能適合因子顛倒測驗，所以最為理想。但此公式仍不適合循環測驗。編制理想指數所需資料繁多，在實際工作中很少套用。世界上只有個別國家在編制進出口商品價格指數時，套用此公式。

基本介紹

• 中文名：費希爾理想公式
• 外文名：Fisher′s formula
• 所屬學科：數學（統計學）
• 提出者：J.費希爾（J.Fisher）
• 相關著作：《統計指數的編制》
• 相關概念：拉斯貝爾斯指數、派許指數等

基本介紹

時間顛倒測驗

時間顛倒測驗亦稱時間互換測驗,指計算期對基期的指數和基期對計算期的指數的乘積應等於1。以公式表示：

上式：代表計算期對基期的指數，稱為前進指數；代表基期對計算期的指數，稱為後退指數。

因子顛倒測驗

因子顛倒測驗亦稱因子互換測驗，指物價指數和相應的物量指數的乘積應等於其價值指數。以公式表示：

式中：代表物價指數，代表物量指數，代表價值指數。

循環測驗

循環測驗指第一個時期對基期的指數和第二個時期對第一個時期指數的乘積，應等於第二個時期對基期的指數。以公式表示：

式中：為第一個時期對基期的指數；為第二個時期對第一個時期的指數；為第二個時期對基期的指數。

拉斯貝爾斯指數

拉斯貝爾斯指數簡稱拉氏指數，是指用基期的銷售額作為權數，對個體價格指數求加權算術平均數，得出個綜合價格指數公式；同時，用基期銷售額(或產值)對個體物量指數求加權算術平均數，得出一個與價格綜合指數相對應的綜合物量指數的方法。這兩個指數都是德國人拉斯貝爾斯於1864年提出的。拉斯貝爾斯兩個綜合指數的基本公式是：

拉氏價格指數公式：

拉氏物量指數公式：

拉氏指數公式可由三種加權取得。

1. 以加權的綜合式即得到拉氏式：

2. 以加權的算術平均式，也可得到拉氏式：

3.以加權的調和平均式，也可得到拉氏式：

派許指數

派許指數簡稱派氏指數，是指用報告期的銷售額作為權數，對個體價格指數求加權算術平均數，得出一個綜合價格指數公式；同時；用報告期銷售額對個體物量指數求加權算術平均數，得出一個與價格綜合指數相對應的綜合物量指數的方法，這兩個指數是德國人派許於1874年提出的。派許的兩個綜合指數的基本公式是:

派氏價格指數公式：

派氏物量指數公式：

派氏公式可由三種加權所得。

1. 以加權的綜合式，即得派氏式：

2. 以加權的算術平均式，也可得到派氏式：

3. 以加權的調和平均式，也可得到派氏式：