貓群算法

貓群算法是近幾年來提出的又一種新型的群體智慧型最佳化計算方法。是群體智慧型算法的一種。是通過將貓的搜尋和跟蹤兩種行為結合起來, 提出的一種解決複雜最佳化問題的方法。

基本介紹

• 中文名：貓群算法
• 外文名：Cat Swarm Optimization
• 縮寫：CSO

基本貓群算法

貓群算法( Cat Swarm Optimization,縮寫為CSO) 是由Shu - An Chu 等人在2006 年首次提出來的一種基於貓的行為的全局最佳化算法。根據 生物學分類,貓科動物大約有 32 種,例如: 獅子、老虎 、豹子 、貓等。儘管生存環境不同 ,但是貓科動物的很多生活習性非常相似。貓的警覺性非常高,即使在休息的時候也處於一種高度的警惕狀 態,時刻保持對周圍環境的警戒搜尋; 它們對於活動的目標具有強烈的好奇心,一旦發現目標便進行跟蹤,並且能夠迅速地捕獲到獵物。貓群算法正是關注了貓的搜尋和跟蹤兩種行為。

貓群算法中,貓即待求最佳化問題的可行解。貓群算法將貓的行為分為兩種模式,一種就是貓在懶散、環顧四周狀態時的模式稱之為搜尋模式; 另一種是在跟蹤動態目標時的狀態稱之為跟蹤模式。貓群算法中,一部分貓執行搜尋模式,剩下的則執行跟蹤模式,兩種模式通過結合率 MR( Mix- ture Ratio) 進行互動,MR 表示執行跟蹤模式下的 貓的數量在整個貓群中所占的比例,在程式中 MR 應為一個較小的值。利用貓群算法解決最佳化問題,首先需要確定參與最佳化計算的個體數,即貓的數量。每隻貓的屬性( 包括由 M 維組成的自身位 置) 、每一維的速度、對基準函式的適應值及表示貓是處於搜尋模式或者跟蹤模式的標識值。當貓進行完搜尋模式和跟蹤模式後,根據適應度函式計算它們的適應度並保留當前群體中最好的解。之後再根據結合率隨機地將貓群分為搜尋部分和跟蹤部分的貓,以此方法進行疊代計算直到達到預設的疊代次數。

數學描述

搜尋模式用來模擬貓的當前狀態,分別為休息、四處查看、搜尋下一個移動位置。在搜尋模式中,定義了 4 個基本要素: 記憶池( SMP) 、變化域 ( SRD) 、變化數( CDC) 、自身位置判斷( SPC) 。 SMP 定義了每一隻貓的搜尋記憶大小,表示貓所搜尋到的位置點,貓將根據適應度大小從記憶池中選擇一個最好的位置點。SRD表示選擇域的變 異率,搜尋模式中,每一維的改變範圍由變化域決定,根據經驗一般取值為 0. 2。CDC 指每一隻貓將要變異的維數的個數,其值是一個從 0 到總維數之間的隨機值。SPC 是一個布爾值,表示貓是否將已經過的位置作為將要移動到的候選位置之一,其值不影響 SMP 的取值。

搜尋模式過程描述

( 1) 將當前位置複製 j 份副本放在記憶池中,j = SMP,即記憶池的大小為 j; 如果 SPC 的值為真, 令 j = ( SMP - 1) ,將當前位置保留為候選解。


( 2) 對記憶池中的每個個體副本,根據 CDC 的大小,隨機地對當前值加上或者減去 SRD% ( 變 化域由百分率表示) ,並用更新後的值來代替原來的值。( 3) 分別計算記憶池中所有候選解的適應度值。


( 4) 從記憶池中選擇適應度值最高的候選點來代替當前貓的位置,完成貓的位置更新。

跟蹤模式過程描述

跟蹤模式用來模擬貓跟蹤目標時的情況。通過改變貓的每一維的速度( 即特徵值) 來更新貓的位置,速度的改變是通過增加一個隨機的擾動來實現的。

( 1) 速度更新。整個貓群經歷過的最好位置, 即目前搜尋到的最優解,記做 Xbest 。每隻貓的速度記做vi ={vi1,vi2,...,vid},每隻貓根據公式(1) 來更新自己的速度。

vi,d(t+1) = vi,d(t) +r* c* (Xbest,d(t)-xi,d(t)), d = 1 ,2 ,... ,M ( 1 )

vi,d( t +1) 表示更新後第 i 只貓在第 d 維的速 度值,M 為維數大小; Xbest,d ( t) 表示貓群中當前具 有最好適應度值的貓的位置; xi,d ( t) 指當前第 i 只 貓在第 d 維的位置,c 是個常量,其值需要根據不 同的問題而定。r 是一個[0,1]之間的隨機值。( 2) 判斷每一維的速度變化是否都在 SRD 內。給每一維的變異加一個限制範圍,是為了防止其變化過大,造成算法在解空間的盲目隨機搜尋。SRD 在算法執行之前給定,如果每一維改變 後的值超出了 SRD 的限制範圍,則將其設定為給定的邊界值。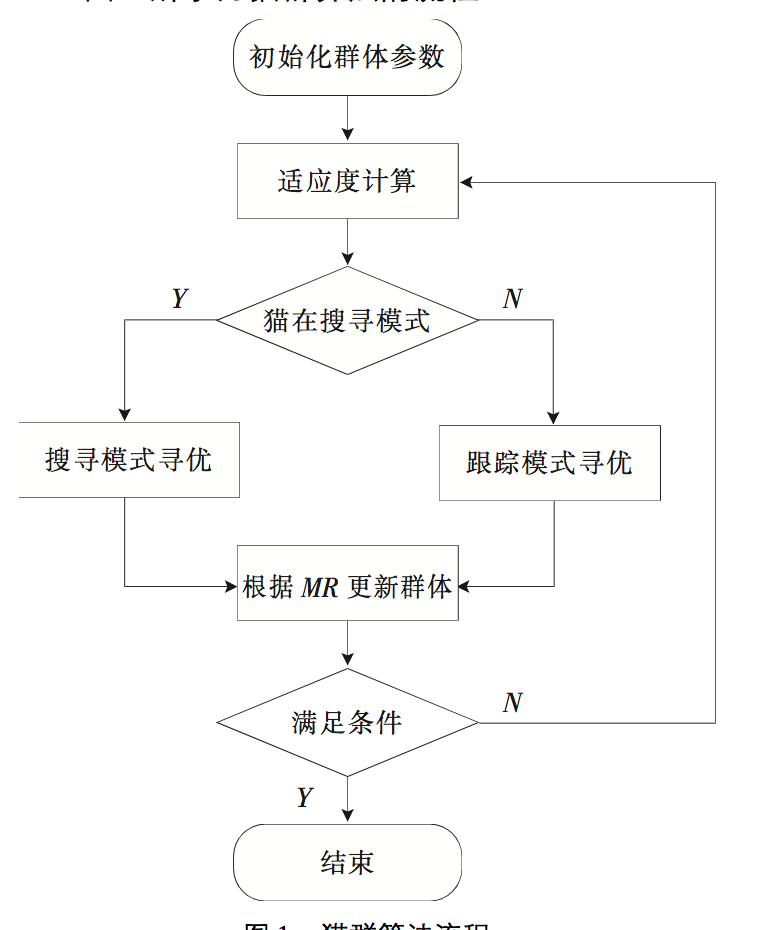

流程圖

( 3) 位置更新。根據公式( 2) 利用更新後的 速度來更新貓的位置。

國內外研究進展

貓群算法由Shu - An Chu 等人在2006 年首次提出,國外學者從該算法的改進和套用方面 做了初步研究,國內對該算法的研究始於近兩年, 因此相關的研究成果很少。但是作為一種新型的 群體智慧型最佳化算法,貓群算法的研究在國內外必將受到廣泛關注。

算法改進研究

Santosa Budi 等( 2009 年)提出一種基於聚類問題的貓群算法,對貓群最佳化公式進行修正,提高了貓群算法最佳化聚類問題的最佳化性能。Yong - Guo Liu 等( 2010 年)引入最新的元啟發式方法到貓群算法中,用以尋找最優的數據集聚類方法。利用搜尋模型和追蹤模型開發和探索解空間,引入K - Harmonic 均值操作改善種群並促進 聚類算法的收斂,提出了 2 種基於貓群算法的聚類方法,分別為貓群最佳化聚類法、K - harmonic 均值貓群最佳化聚類法。范凱波( 2011 年)通過研究群體智慧型計算,提出了基於貓群算法最佳化的 k - 均值聚類 算法,實現了車輛目標的分類。Orouskhani Maysam 等( 2011 年)為提高貓群算法的收斂性,在位置更新方程內增加一個新的參數作為慣性加權,在算法的追蹤模型中使用新的速率更新方程,提出一種加權平均慣性貓群算法。

Pradhan Pyari Mohan 等( 2012年)通過擴展已有的貓群算法提出一種新的多目標進化算法。該 算法利用 Pareto 支配的概念沿著尋優過程找到非支配解,並將這些非支配解外置存檔。仿真結果表明該方法是解決多目標問題的一種較好途徑。Shi - DaYang 等( 2013年)針對全局最佳化問題提出一種改進的混沌貓群算法。利用不同混沌映 射改進搜尋模型的步長,研究 7 種不同的混沌映射,找到最佳的物流與正弦圖。

並行算法結構研究

Pei - Wei Tsai 等( 2008 年)研究了貓群算法的並行結構,設計了並行貓群算法。在種群規 模較小和總疊代次數較少的情況下,並行貓群算法能有效提高收斂速度。Pei - Wei Tsai 等( 2012 年)為了在較小種群規模和較少疊代次數條件下解決數值最佳化問題,在並行貓群算法的追蹤過程中引入田口方法,提出了一種最佳化精度高、計算速度快的強化並行貓群算法,並將其套用於解決飛機計畫恢復問題,取得了較好的套用效果。

混合算法研究

Pei - Wei Tsai 等( 2010 年)提出一種基於貓群算法和人工蜂群算法的混合最佳化算法,通過 測試 5 種基準函式,證明了混合算法的精確性、收斂性、快速性和穩定性。Li Ming 等( 2013 年)針對粒子群最佳化算法在整個疊代過程中易陷入局部最優、在疊代後期收斂速度慢的缺點,提出一種基於貓圖的粒子群最佳化算法。基於貓圖的遍歷性 和規律性,粒子可以被均勻地分散到整個尋優空 間,增加了粒子的多樣性。同時,使用粒子的局部 濃度策略適應性地調整慣性權重,從而提高收斂 速度。粒子濃度較大時,利用較小的慣性權重來 增強局部搜尋能力,粒子濃度較小時,利用較大的慣性權重來增強算法的全局搜尋能力。Shi - Da Yang 等( 2013 年)為解決全局最佳化問題,基於同倫算法的概念,提出一種受同倫算法啟發的貓 群算法。根據最佳化函式的因變數,跟蹤一條從簡單問題解到由同倫算法給出的問題解的路徑。這種策略能提高貓群算法的尋優效率。

算法套用研究

王光彪等( 2011 年)針對傳統進化算法在圖像分類中存在的收斂速度慢、易陷入局部最優等問題,提出用貓群算法求解圖像分類問題,將求解組合最佳化問題轉化為貓群的位置尋優過程,並 分析了貓群算法及其兩種行為模式下的算法模型。驗證了貓群算法在圖像分類中的準確性和有效性。Panda Ganapati 等( 2011 年)將IIR系統識別任務描述為一種最佳化問題,引入貓群算法改 進此模型的以新種群為基礎的學習規則。Kalai- selvanG等(2011年)嘗試使用貓群最佳化技術將水印恢復至原始狀態。通過修正轉換係數的最少有效位可以獲取頻域中的嵌入式水印。套用四捨五入方法將圖像中隱藏的水印從原始水印中恢 復出來,引入群體智慧型技術來消除由簡單方法將 圖像從頻域轉移到空間域時產生的捨入誤差。Zhi-HuiWang等(2012年)針對最低有效位替換方法解決隱秘圖像問題時運行時間長的問 題,通過改進貓群最佳化策略來獲取解決隱秘圖像 質量問題的最優解或次優解。Pradhan Pyari Mo- han 等( 2012 年)將各個無線認知機的質量和 決策閾值的選擇描述為一個約束誤報和檢測機率 互為矛盾的多目標最佳化問題,將多目標貓群算法套用於協作頻譜感知領域。Long Xu 等( 2012 年)針對資源受限項目調度問題提出一種基於貓群算法的方法。通過貓的多維位置提供解決資源受限項目調度問題的潛在方案,包括 3 個步驟: 先隨機初始化貓的參數,然後疊代位置,通過串列 SGS 方法計算適應度,最後如果條件滿足則終止程式。Deivaseelan. A 等( 2012 年)引入改進的貓群算法改進 IIR 系統識別模型的以新種群為基礎的學習規則。Shi - Yu Cui 等( 2013 年) 針對原始塊截斷編碼方法的複雜性難以找到有效的常用點陣圖,利用貓群算法進行塊截斷編碼,提出一種基於此種編碼方式的圖像壓縮技術。

貓群算法的研究剛剛起步,一些思想處於萌芽階段,嚴格的理論基礎尚不成熟。對於算法本身的思想、原理、參數設定以及種群多樣性的研究,仍停留在實驗探索階段,並未有更深入的分析與討論。關於算法收斂性的分析與證明的研究還未出現。對貓群算法的改進技術主要集中於常態的增加參數、加入部分操作運算元等方面,對於算法框架、疊代進化方式等的改進的研究較少。部分學者將粒子群算法以及混沌搜尋等算法 或思想引入貓群算法,在一定程度上提高了算法的最佳化性能,但仍然存在易陷入“早熟”、運行速度 慢等缺陷,並且,被引入算法僅執行貓群算法的單個行為。針對貓群算法最佳化組合最佳化問題的離散模型的研究還未出現。目前貓群算法主要在圖像處理、數據挖掘領域的實際問題中得到了較多的套用,在其它領域中的套用仍處於初級階段,尚不成熟,甚至尚未涉及,尤其是在農業工程領域的套用研究尚未出現。