基本介紹
- 中文名:貓映射
- 別名:Arnold映射
- 提出者:弗拉基米爾·阿諾德
- 定義:Arnold授課的時候經常使用貓的圖像作為例子,故稱為“貓映射”。
公式













例子







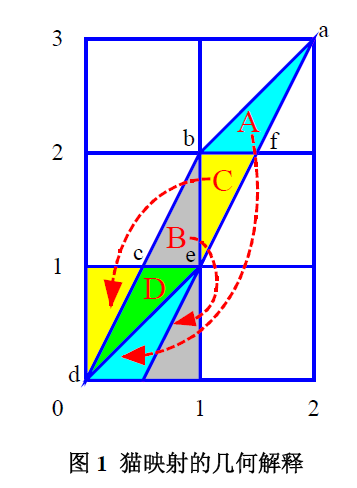

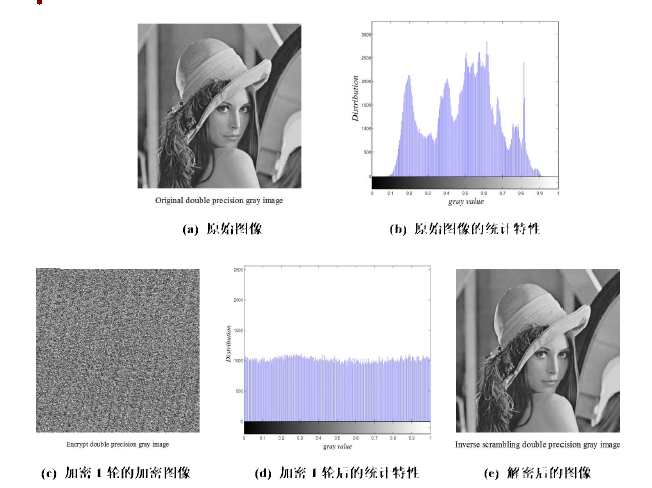
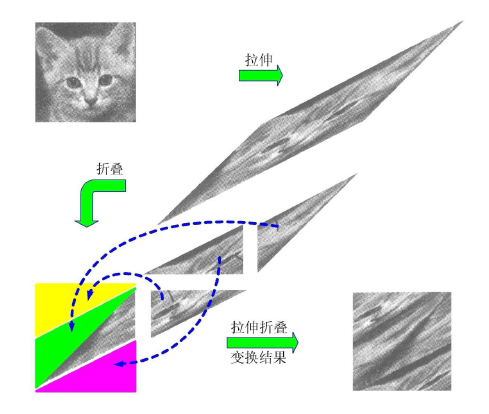























貓映射(Cat映射),也稱為Arnold映射,由俄國數學家弗拉基米爾·阿諾德(Vladimir Igorevich Arnold)提出,在Arnold授課的時候經常使用貓的圖像作為例子,故稱為“貓映射”。這是一種在有限區...
貓臉映射 貓臉映射(cat map [of Arnosov])是1993年經全國科學技術名詞審定委員會審定發布的力學名詞。發布時間 1993年經全國科學技術名詞審定委員會審定發布的力學名詞。出處 《力學名詞》
的80連線埠就叫做映射連線埠。連線埠映射就是靜態PAT(連線埠地址轉換)。把區域網路某個PC的連線埠號固定發布在公網IP里。把A的1連線埠 映射到B的 2連線埠上。當有機器訪問B的2連線埠時 就直接跳轉到A的1連線埠。不知道這樣說對不,一般連線埠映射是在路由器上或防火牆上做。連線埠映射 區域網路的一台電腦要上網際網路對外開放服務或接收數據...
主要內容包括:數學預備知識與混沌基本概念、離散時間系統的反控制-Chen-Lai算法、離散時間系統的反控制-Wang-Chen算法、離散時間系統的反控制-Wang-Chen算法、單峰和多峰映射、離散正弦多峰映射、線性取模運算多峰映射、混沌控制與同步、一類離散時間混沌系統的構造、同步及套用、高維廣義貓映射及其在圖像加密中的套用、...
映射語言是以.NET為中心的,意味著映射是按照持久化類的定義來創建的,而非表的定義。在Hibernate中XML映射文檔可以手動定義,也有一些工具來輔助生成,包括Xdoclet、Middlegen和AndroMDA,但是在NHibernate文檔中並沒有上述的輔助工具,不過可以採用MyGeneration這樣的代碼生成工具來生成XML配置文檔。雖然NHibernate目前不...
3、很好地支持TDM業務。TDM 業務映射到GEM 幀中, 由於GPON TC 幀幀長為 125 μs, 能夠直接支持TDM 業務。TDM 業務也可映射到ATM 信元中, 也能提供有QoS 保證的實時傳輸。4、簡單、高效的適配封裝。採用GEM 對多業務流實現簡單、高效的適配封裝。在 APON 中, 所有的多業務流(話音、數據業務流) 都必需進行...
相互映射 某一劇院專以經營某劇而聞名,比如《西貢小姐》是在百老匯劇院演出的,而《美女與野獸》就在新阿姆斯特丹劇院上演。百老匯音樂劇演出的經營與運作很有特色,即劇院與劇目之間的映射關係非常明顯,某一劇院專以經營某劇而聞名,這種運作方法其實也是由於音樂劇本身舞台、燈光等製作的複雜性,這些固定的道具布景...
