警戒限

警戒限(warning limits)一般在控制圖的控制限的內側，位於中心線上下二個標準差處。若所描的點超出警戒限，但未超出控制限，雖然不一定需要立即停止生產去查找原因， 但工序應注意可能有不可忽視的原因。

基本介紹

• 中文名：警戒限
• 外文名：warning limits
• 所屬學科：數學
• 所屬問題：統計學（統計質量管理）
• 簡介：控制圖的界限
• 符號表示：UWL和LWL

基本概念

警戒限是控制圖的界限。當測試系統處於統計控制狀態時，大多數測定結果落在此範圍內(95%的可能性)；若超出此界限時，就警告檢驗人員應檢查原因。

警戒限是位於控制圖的中心線和控制限之間的兩條直線，分別以UWL和LWL表示。通常，控制限 叫做行動限，而警戒限定為 。

具警戒限控制圖的分析

建立警戒限的目的是容易理解的，如果樣本平均值 超過行動限，那么我們就可以十分有把握地相信生產過程有缺陷。但是當接連著有若干個點子位於行動限之內，而又離開行動限不遠時，能否作出生產過程處於控制狀態的結論?利用只有警戒限的控制圖能解決這個問題。

在比較幾個控制圖的優劣時，作為衡量標準的重要的量是過程發生惡化和發信號之間的時間長度，或者發信號前所觀測的樣本數量，這個樣本數量叫做鏈長(或遊程長度)。當生產過程被認為滿意時，我們希望在接受信號前有很多樣本，亦即當分布的中心位於 上時，我們需要很長的鏈長；當過程已遠離中心值 時，我們需要立即發信號，亦即需要很短的鏈長。所以平均鏈長也是控制圖相對效率的度量。

操作特性曲線是度量顯著性檢驗功效的良好方法，常規控制圖的功效可用這種曲線來衡量，但對一些特殊控制圖，例如具有警戒限圖和累積和圖，它就不是一個有效的度量，因為利用這兩個圖形時點子超出界限的機率依賴於以前平均值或總和的位置。這時平均鏈長是相對效率較好的度量。

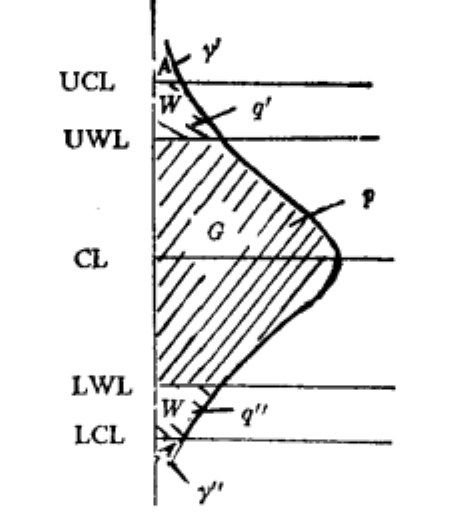
設總體服從常態分配 ，其中m為未知， 為已知，我們考慮具有行動限和警戒限的平均值控制圖。在圖上描繪子樣本的平均值。這種圖可分為3個區域：行動域、警戒域和良好域，分別記作A、W和G，如圖1所示。位於行動域內的平均值表明過程水平極端遠離中心值，以致必須立即採取糾正動作，位於警戒域內的平均值表明過程水平離開中心值不太遠，但是連續好幾個樣本平均值位於此區域內則認為產品質量惡化；位於良好域內的平均值說明生產條件沒有顯著變化。常規控制圖根據一個點子位於行動域就發信號，而具有警戒限的的 圖根據一個點子位於行動域或k個接續點子位於警戒域(或下警戒域)而發信號。

帶警戒限的均值控制圖適用於過程標準差已知的條件下，對過程均值進行控制，有其特殊的優越性。

表1 帶警戒限均值控制圖的符號及定義

帶警戒限的均值控制圖適用於過程標準差已知的條件下，對過程均值進行控制，有其特殊的優越性。 L——平均鏈長，即當生產過程的均值保持在某一數值時，在控制圖上得到失控信號時，所描出的樣本點的平均數。直觀 意義是當質量特性值不變時，工藝過程兩次調整間的平均樣本數； L0——受控過程的平均鏈長，就是過程平均能持續多長時間才誤發一次告警信號，L0=1/α； L1——失控過程的平均鏈長，就是過程平均要滯後多長時間才發出告警信號，即L1=1/(1-β)； CL——中心線； UAL——上行動限； LAL——下行動限； UWL——上警戒限； LWL——下警戒限； μU——過程平均的最大允許值； μL——過程平均的最小允許值； TU——規範上限； TL——規範下限； · μ0——過程均值； σ0——過程標準差； n——樣本大小： K——落在同一側行動界限和警戒限間的，判過程為失控的樣本連續點數； δ——標準偏移量； 當均值上偏時，δ=（μU-μ0）/σ0；當均值下偏時， δ=（μ0-μL）/σ0。 p1——不合格品率最大允許值； B1——計算行動限所用係數； B2——計算警戒限所用係數。

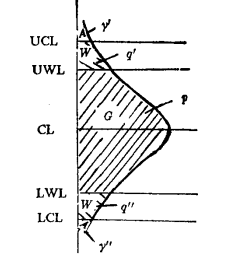
圖1 具有警戒限控制圖

我們作如下規定：如果有一點超出行動限或連續兩點位於警戒限和行動限之間，則採取糾正措施。設一點位於兩警戒限之間的機率為p，位於警戒限和行動限之間的機率為q，位於行動限之外的慨率為r，顯然p+q+r=1。於是樣本平均鏈長為

利用鏈長對常規的圖和具有警戒限的圖做比較，通過計算可以得出：同常規的圖相比，具有警戒限的圖對於過程平均值的微小變化具有較小的ARL值，因而它是更敏感的。自然，當異常原因不存在時，這導致尋找原因的費用的增加，但是當δ=0時這種不必要尋找的機率僅為0.5%，是常規的圖的不必要尋找機率的1.7倍。當平均值變至時，這兩種圖形的敏感性是近似相同的。隨著過程平均值的變大，ARL值變小，因而具有警戒限的圖的敏感性降低。警戒限可作為常規控制圖的補充。