謂詞變元代入規則

狹謂詞演算HA系統中的初始變形規則。公式A中一謂詞變元，可處處由一公式B替代，為此謂詞變元是n項的，則B中必須至少有n個個體變元。

概念定義

定義一

狹謂詞演算HA系統中的初始變形規則。國內一種有影響的表述是:在公式A中的n元謂詞變元Γ(Δ₁,Δ₂,…,Δ_n)可以處處代之以一複合謂詞B(Δ₁,…,Δ_n,Δ_n+1,…,Δn+m)(m≥0)。代入的結果可以記為:

如果├A,那么

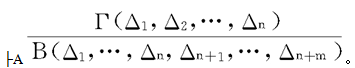
定義二

謂詞(和函詞變元)公式等價變換的規則之一.先將大小代入式都改名(參見“改名”),使得大小代入式的約束變元與對方的一切變元(自由或約束)都不相同,然後做出小代入式的相應填式,再把這些填式代入到代入變元的相應填式處. 例如,要在公式(ᗄx)[Axz→Bx](此處A,B均為謂詞)中把α(e₁,e₂,x)代入A_e1,e₂,根據上述原則,先將大代入式改名,得(ᗄu)[Auz→Bu],然後將小代入式α(e₁,e₂,x)代入得(ᗄu)[α(u,z,x)→Bu].

規則要點

(1)代入的結果必須是合式公式。

(2)A中的自由個體變元,代入後不得為B中量詞所約束。

(3)結果m>0,B(Δ₁,…Δ_n,Δ_n+1,…,Δ_n+m)中的變元Δ_n+1,…,Δ_n+m等在代入後不得為A中原有的量詞所約束。

違反這些要求,代入後的公式就可能不合式,或者不能保持普遍有效。

實例分析

例1:設在“F(x)→F(x)∨G(y)”中,用(ᗄy)R(Δ,y)代F(Δ),得(ᗄy)R(x,y)→(ᗄy)R(x,y)∨G(y)。這裡y既約束,又自由,所以不合式。違反了要求(1)。

例2:設在普遍有效式(ᗄx)F(x)→F(y)中,用(∃y)R(Δ,y)代F(Δ),可得(ᗄx)(∃y)R(x,y)→(∃y)R(y,y)。由於違反要求(2),代入後的公式不普遍有效。