諾頓定理(Norton's theorem)：含獨立源的線性電阻單口網路N，就連線埠特性而言，可以等效為一個電流源和電阻的並聯。電流源的電流等於單口網路從外部短路時的連線埠電流isc；電阻R0是單口網路內全部獨立源為零值時所得網路N0的等效電阻。
基本介紹
- 中文名：諾頓定理
- 外文名：Nortons theorem
- 對偶定理：戴維南定理
- 注意事項1：只對外電路等效，對內電路不等效
- 注意事項2：只適用於線性的有源二端網路
- 領域：電子電路
定義,簡介,證明,注意事項,諾頓等效電路的計算,轉換至戴維寧等效電路,諾頓等效電路的範例,
定義
諾頓定理（Norton's theorem）指的是一個由電壓源及電阻所組成的具有兩個端點的電路系統，都可以在電路上等效於由一個理想電流源I與一個電阻R並聯的電路。對於單頻的交流系統，此定理不只適用於電阻，亦可適用於廣義的阻抗。諾頓等效電路是用來描述線性電源與阻抗在某個頻率下的等效電路，此等效電路是由一個理想電流源與一個理想阻抗並聯所組成的。
諾頓定理是戴維寧定理的一個延伸，於1926年由兩人分別提出，他們分別是西門子公司研究員漢斯·梅耶爾（1895年-1980年）及貝爾實驗室工程師愛德華·勞笠·諾頓（1898-1983）。實際上梅耶爾是兩人中唯一有在這課題上發表過論文的人，但諾頓只在貝爾實驗室內部用的一份技術報告上提及過他的發現。
簡介
諾頓定理與戴維南定理互為對偶的定理。定理指出，一個含有獨立電源線性二端網路N(圖1a), 就其外部狀態而言,可以用一個獨立電流源isc和一個鬆弛二端網路N0的並聯組合來等效(圖1b)。其中，isc是網路N的短路電流，鬆弛網路N0是將網路 N中的全部獨立電源和所有動態元件上的初始條件置零後得到的網路。上述並聯組合稱為諾頓等效網路。在復頻域中等效網路由電流源Isc和運算元阻抗Yi(s)並聯而成（圖2）。Isc(s)是短路電流的拉普拉斯變換，Yi(s)是鬆弛網路N0的入端（策動點）導納。另外，還能導出網路N用於正弦穩態分析和直流分板的等效網路。
求等效電路的關鍵是求出網路N的短路電流和網路N0的入端（策動點）導納。它們均可通過電子計算機求得。
isc稱為短路電流。Ro稱為諾頓電阻，也稱為輸入電阻或輸出電阻。電流源isc和電阻Ro的並聯單口，稱為單口網路的諾頓等效電路。在連線埠電壓電流採用關聯參考方向時，單口的VCR方程可表示為i=u/Ro+ isc
諾頓定理和戴維南定理是最常用的電路簡化方法。由於戴維南定理和諾頓定理都是將有源二端網路等效為電源支路，所以統稱為等效電源定理或等效發電機定理。
證明
在單口網路連線埠上外加電壓源u，根據疊加定理，連線埠電壓可以分為兩部分組成。分別求出外加電壓源單獨產生的電流i’=u/Ro和單口網路內全部獨立源產生的電流i"=-isc，然後相加得到連線埠電壓電流關係式：i=i’ +i”=u/Ro+isc
諾頓定理證明
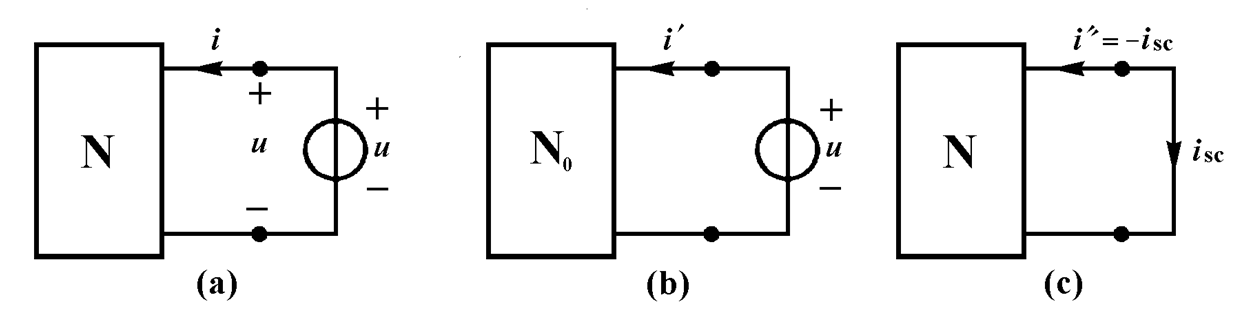諾頓定理證明注意事項
（1）諾頓定理只對外電路等效，對內電路不等效。也就是說，不可套用該定理求出等效電源電動勢和內阻之後，又返回來求原電路（即有源二端網路內部電路）的電流和功率。
（2）套用諾頓定理進行分析和計算時，如果待求支路後的有源二端網路仍為複雜電路，可再次運用諾頓定理，直至成為簡單電路。
諾頓定理
諾頓定理（3）諾頓定理只適用於線性的有源二端網路。如果有源二端網路中含有非線性元件時，則不能套用諾頓定理求解。
諾頓等效電路的計算
任何只包含電壓源、電流源及電阻的黑箱系統，都可以轉換成諾頓等效電路
要計算出等效電路，需：
- 在AB兩端短路（亦即負載電阻為零）的狀況下計算輸出電流IAB。此為INO。
- 在AB兩端開路（在沒有任何往外電流輸出，亦即當AB點之間的阻抗無限大）的狀況下計算輸出電壓VAB，此時RNo等於VAB除以INO。
- 此等效電路是由一個獨立電流INO與一個電阻RNO並聯所組成。
其中的第2項也可以考慮成：
- 2a.將原始電路系統中的獨立電壓源以短路取代，而且將獨立電流源以開路取代。
- 2b.若電路系統中沒有非獨立電源的話，則RNo為移走所有獨立電源後的電阻*。
轉換至戴維寧等效電路
- 左邊是諾頓等效電路，右邊是戴維寧等效電路，可用下列方程將諾頓等效電路轉換成戴維寧等效電路：
諾頓等效電路的範例
在此範例中，先將A、B兩點短路，整體電流
可以寫成：
利用電流的分流原則，從
流過負載的電流
為：
再把電壓源用短路來取代，從系統開口兩端往裡看的等效阻抗為：
因此，等效電路則是由一個3.75 mA的電流源並聯一個2KΩ的電阻所組成。
