基本介紹
- 中文名：誤差距離
- 外文名：Error distance
- 影響：點源的分布距離
- 模型1：考慮角測量誤差
- 模型2：飛彈不沿中垂線入射時
- 模型3：非相干兩點源功率不等時
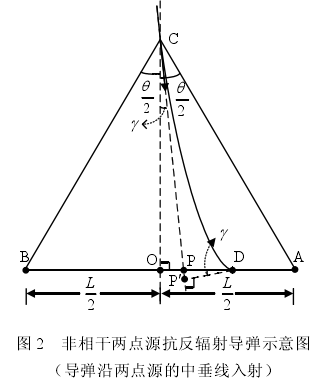
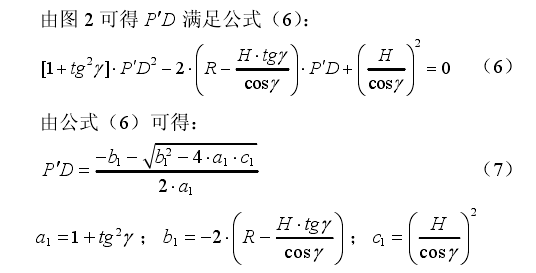
反輻射飛彈誤差距離的研究進展,反輻射飛彈的誤差距離模型,考慮角測量誤差的誤差距離模型,飛彈不沿中垂線入射時的誤差距離模型,非相干兩點源功率不等時的誤差距離模型,
反輻射飛彈誤差距離的研究進展
反輻射飛彈主要通過單脈衝導引頭來實現對目標雷達的測向與定位，兩點源（或多點源）干擾能夠有效的干擾其單脈衝導引頭，從而成為現代雷達對抗反輻射飛彈的主要技術措施之一。所謂兩點源干擾，就是在所保護雷達的附近另設一個與雷達頻率相同的誘餌輻射源：輻射源與雷達信號的相位無關時（稱為非相干兩點源），反輻射飛彈導引頭跟蹤兩點源的功率重心；輻射源與雷達信號的相位相關、相位差為π時（稱為相干兩點源），反輻射飛彈導引頭跟蹤兩點源之外的某一點。由於輻射源信號相干的實現難度較大，現代雷達配置的都是非相干輻射源。
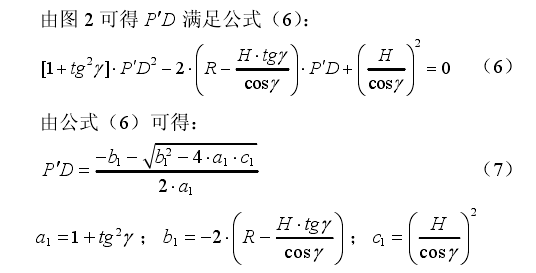
雷達採用非相干兩點源干擾措施時，反輻射飛彈的誤差距離與點源的分布距離有關。國內已有多篇公開發表的文獻，對雷達與干擾源的配置距離、反輻射飛彈的誤差距離及其它相關模型進行了研究。然而，目前的研究成果中還存在以下幾點不足：（1）沒有考慮反輻射飛彈導引頭的角測量誤差（又稱角跟蹤精度，一般為1°~3°）對誤差距離的影響；（2）θ為等功率兩點源相對於反輻射飛彈導引頭天線的夾角，在兩點源法平面與反輻射飛彈瞄準軸（即兩點源與反輻射飛彈夾角的角平分線）夾角為α時，現有文獻均將圖1中的O′點近似為O點，從而使AB′≈AB·cosα，這種近似在α和θ改變時會引起一定的誤差；（3）現有文獻多是針對等功率非相干兩點源進行研究，沒有給出一個實用的不等功率非相干兩點源條件下的反輻射飛彈誤差距離模型。
反輻射飛彈的誤差距離模型
考慮角測量誤差的誤差距離模型
公式(1)中，反輻射飛彈導引頭的角測量誤差γ不為0時：
PD=P′D/cos(γ)（5）
由圖2可得P′D滿足公式（6）：
將公式（5）和（7）代入公式（1），可得反輻射飛彈沿兩點源中垂線入射時的誤差距離模型。由公式（1）、（5）和（7）可以看出，反輻射飛彈雷達導引頭的角跟蹤精度γ直接影響著飛彈的誤差距離。
飛彈不沿中垂線入射時的誤差距離模型
在實際作戰過程中，反輻射飛彈常以一定的角度對目標雷達實施攻擊，當兩點源的法平面與反輻射飛彈的瞄準軸（即兩點源與反輻射飛彈夾角的角平分線）夾角為α時，令L′=AB′，由三角公式可得：
公式（9）修正了文獻中的L′=L·cosα所帶來的誤差。可得反輻射飛彈的誤差距離為：
將H′代入公式（5）和（6）可得：
非相干兩點源功率不等時的誤差距離模型
在實際作戰過程中，兩點源要做到在反輻射飛彈處的功率完全相等難度很大，通常為了保護雷達，常使誘餌的功率稍大於雷達旁瓣的功率。假設點源A的功率PA大於點源B的功率PB。首先考慮反輻射飛彈沿兩點源的中垂線入射時的情況。由文獻可知，在開始跟蹤時，反輻射飛彈到兩個目標的距離大大超過兩點源之間的間距L，此時兩點源與反輻射飛彈的夾角小於某一角度φ(在實際計算時可認為φ=γ)，導引頭跟蹤兩點源的幾何中心O；隨著飛彈與兩點源的接近，兩點源與反輻射飛彈的夾角不斷增大，當增加到角度φ時，反輻射飛彈開始跟蹤兩點源的功率重心O′′；當兩點源與反輻射飛彈的夾角增大到θ=0.8~0.9·θR時，飛彈開始跟蹤點源A，並以最大過載向A點轉彎，最後命中點D。假設反輻射飛彈在點C′的時刻為0，在點C的時刻為T。由文獻可知，飛彈從點C′運動到點C的過程中，飛彈的瞄準軸與飛彈和兩點源連線的夾角ωA、Bω始終滿足公式：ωA/ωB=PB2/PA2。（此處忽略了兩點源到反輻射飛彈的距離不同所引起的不同功率損耗），所以飛彈在0~T之間的運動滿足下列方程組：
由公式（12）進行仿真推算可得：
將公式(11)代入(13)可得，非相干兩點源功率不等條件下，反輻射飛彈不沿兩點源中垂線入射時的誤差距離模型。
