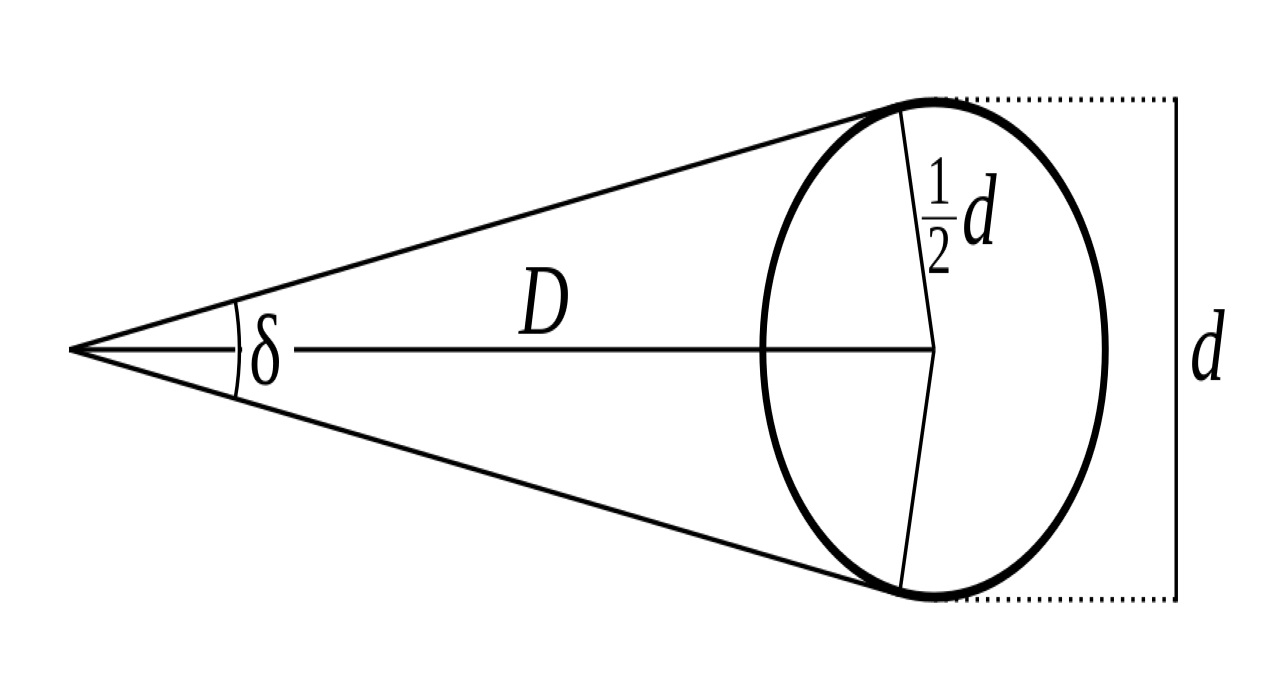
角直徑是以角度做測量單位時,從一個特定的位置上觀察一個物體所得到的"視直徑"。
基本介紹
- 中文名:角直徑
- 外文名:Angular diameter
公式,
視直徑只是被觀測的物體在垂直觀測者視線方向中心的平面上產生的透視投影的直徑。由於它是在觀測者的角度下按比例的縮影,因此與物體真實的直徑會有所不同。
δ=(206,265)d / D arcseconds
δ:角直徑
d:物體直徑
D:物體距離
arcseconds:角秒(或稱弧秒)
公式

角直徑公式圖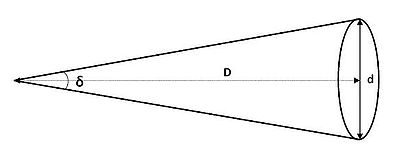

其中是角直徑, d 是物體的實際直徑,D 是到物體的距離 ;δ 的單位是弧度



當D遠大於d時,公式可簡化為

對於直徑等於實際直徑的球形物體,可得到角直徑公式%5Cdelta%3D1arcsin%5Cleft(%5Cfrac%7Bd%7D%7B2D%7D%5Cright)</math></p><p>實際套用時,小角度近似值適於X遠小於1的時候:arcsinΧ≈arctanΧ≈Χ</p><h2>用於天文學</h2><p>在<a>天文學中</a>,<a>天體</a>的大小通常根據從<a>地球</a>看到的角直徑給出,而不是它們的實際尺寸。</p><p>由於這些角直徑通常較小,因此通常以<a>弧秒</a>(“)表示它們</p><p>弧秒是1<a>度</a>(1°)的1/3600,1弧度是180 /π度,所以1個弧度等於3,600 * 180 /π<math>{\ displaystyle \ pi}arcseconds,大約是206,265弧秒
因此,物理直徑d在距離D處的物體的角直徑,以弧秒表示,可由下式給出
δ=(206,265)d / D arcseconds
這些物體的角直徑為1“:
因此,從1 pc的距離看,地球繞太陽軌道的角直徑是2“,因為1 AU是地球軌道的平均半徑。