若一條線段對兩點所張的視角相等,則這兩個角的頂點與線段的兩個端點四點共圓。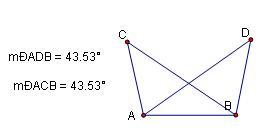

即圖中∠ACB=∠ADB,則A、B、C、D四點共圓。
證明:連結CD,設AD,BC相交於O。則
因為 ∠ACB=∠ADB, ∠AOC=∠BOD
所以 △AOC∽△BOD
所以 AO:BO=CO:DO
所以 AO:CO=BO:DO
所以 △COD∽△AOB
所以 ∠CDO=∠ABO
那么 ∠CAB+∠CDB=∠CAB+∠CDO+∠BDO=∠CAB+∠ABO+∠ACB
=180°
即:四邊形一組內對角互補,四邊形內接於圓
命題得證。
