基本介紹
- 中文名:規則溶液理論
- 外文名:Hildebrand solubility parameters
- 別稱:溶解度參數理論
- 特點:總體積保持不變
- 時間:20世紀20年代後期
理論簡介,理論內容,
理論簡介
規則溶液理論於20世紀20年代後期由J.H.希爾德布蘭德建立。其成就在於以純組分的摩爾體積和溶解度參數來計算溶液的過量吉布斯函式以及活度係數,所導出的過量吉布斯函式恆大於零,不適用於對理想溶液負偏差的溶液,比較成功地解釋了碘的溶解度以及某些溶質在相當廣泛的非極性溶劑中的溶解度。
理論內容
該理論的要點為:假定兩種液體分子的大小沒有顯著差別,沒有由於偶極或氫鍵等因素所引起的溶液中分子的特殊取向,分子在溶液中作完全無規則的混合,在等容條件下,摩爾數為n1和n2的兩種液體混合,具有與理想溶液相同的混合熵:
(1)式中 R為氣體常數。混合能由混合物位能與兩種純液體的位能來確定。設液體的摩爾位能與全部分子成對的相互作用能 ε(r)有關,晶體的晶格能是由ε(r)對全部影響所及的晶格求和而得,液體的位能則由一連續的徑向分布函式g(r)積分而得。徑向分布函式是以已知分子為中心,在距離r處發現的另一分子的幾率。對於摩爾數為n的純液體,其蒸發能為:
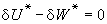 (1)
(1)式中NA為阿伏伽德羅數;V為液體的摩爾體積。對於摩爾數為n1和n2的二元混合液體,其蒸發能為:這裡在理論處理上作了些近似和簡化,包括假定兩個不同種分子的作用能等於兩個同種分子的作用能的幾何平均值: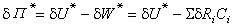 蒸發能
蒸發能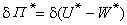 二元混合液體,其蒸發能為
二元混合液體,其蒸發能為
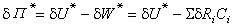 蒸發能
蒸發能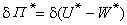 二元混合液體,其蒸發能為
二元混合液體,其蒸發能為ε12=(ε11ε22)┩
可導出兩種非極性液體的混合能ΔEM:
(2)根據定義,混合過程中體積不變,從式(1)和(2)可推導出過量吉布斯函式GE: GE=(x1V1+x2V2)(δ1-δ2)2φ1φ2
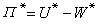 混合能
混合能式中x1和x2為組分的摩爾分數;δ1和δ2為組分的溶解度參數;φ1和φ2為組分的體積分數:活度係數γ1和γ2見下式: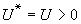 體積分數
體積分數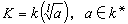 γ1和γ2
γ1和γ2
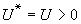 體積分數
體積分數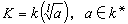 γ1和γ2
γ1和γ2