基本介紹
實例,6174數學黑洞,自冪數,冰雹猜想(角谷猜想),冰雹猜想來歷,強悍的27,驗證規律,卡普雷,簡介,分類,操作演示,
實例
123數學黑洞
123數學黑洞,即西西弗斯串。
西西弗斯串可以用幾個函式表達它,我們稱它為西西弗斯級數,表達式如下:
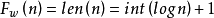
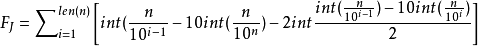
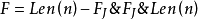
F 是一級原函式,k級通項式為它的疊代循環

 數學黑洞
數學黑洞例如:1234567890,
偶:數出該數數字中的偶數個數,在本例中為2,4,6,8,0,總共有 5 個。
奇:數出該數數字中的奇數個數,在本例中為1,3,5,7,9,總共有 5 個。
總:數出該數數字的總個數,本例中為 10 個。
新數:將答案按 “偶-奇-總” 的位序,排出得到新數為:5510。
重複:將新數5510按以上算法重複運算,可得到新數:134。
重複:將新數134按以上算法重複運算,可得到新數:123。
結論:對數1234567890,按上述算法,最後必得出123的結果,我們可以用計算機寫出程式,測試出對任意一個數經有限次重複後都會是123。換言之,任何數的最終結果都無法逃逸123黑洞。
為什麼有數學黑洞“西西弗斯串”呢?
(1)當是一個一位數時,如是奇數,則k=0,n=1,m=1,組成新數011,有k=1,n=2,m=3,得到新數123;
如是偶數,則k=1,n=0,m=1,組成新數101,又有k=1,n=2,m=3,得到123。
(2)當是一個兩位數時,如是一奇一偶,則k=1,n=1,m=2,組成新數112,則k=1,n=2,m=3,得到123;
如是兩個奇數,則k=0,n=2,m=2,組成022,則k=3,n=0,m=3,得303,則k=1,n=2,m=3,也得123;
如是兩個偶數,則k=2,n=0,m=2,得202,則k=3,n=0,m=3,由前面亦得123。
(3)當是一個三位數時,如三位數是三個偶數字組成,則k=3,n=0,m=3,得303,則k=1,n=2,m=3,得123;
如是三個奇數,則k=0,n=3,m=3,得033,則k=1,n=2,m=3,得123;
如是兩偶一奇,則k=2,n=1,m=3,得213,則k=1,n=2,m=3,得123;
如是一偶兩奇,則k=1,n=2,m=3,立即可得123。
(4)當是一個M(M>3)位數時,則這個數由M個數字組成,其中N個奇數數字,K個偶數數字,M=N+K。
由KNM聯接生產一個新數,這個新數的位數要比原數小。重複以上步驟,一定可得一個三位新數knm。
可用Pascal語言完成:
Var n, j, e, z, z1, j1, t: longint;Begin readln(n); t := 0; repeat e := 0; j := 0; z := 0; while n > 0 do begin if n mod 10 mod 2 = 0 then e := e + 1 else j := j + 1; z := z + 1; n := n div 10; end; if j < 10 then j1 := 10 else j1 := 100; if z < 10 then z1 := 10 else z1 := 100; n := e * j1 * z1 + j * z1 + z; writeln(n); t := t + 1; until n = 123; writeln(’t = ’, t); readln;End.
Python代碼實現:
def num_calculate(str_number): even, ood = [], [] for i in str_number: if int(i) % 2 == 0: even.append(i) else: ood.append(i) str_list = "".join([str(len(even)), str(len(ood)), str(len(even)+len(ood))]) return str_list def BlackHole(str_number): i = 0 number = num_calculate(str_number) while 1: i += 1 print('第{}次:{}'.format(i, number)) number = num_calculate(number) if int(number) == 123: print('第{}次:{}'.format(i, number)) breakif __name__ == '__main__': BlackHole(input("隨意輸入一個數字: "))6174數學黑洞
(即卡普雷卡爾(Kaprekar)常數)
比123黑洞更為引人關注的是6174黑洞值,它的算法如下:
取任意一個4位數(4個數字均為同一個數的,以及三個數字相同,另外一個數與這個數相差1,如1112,,6566等除外),將該數的4個數字重新組合,形成可能的最大數和可能的最小數,再將兩者之間的差求出來;對此差值重複同樣過程,最後你總是至達卡普雷卡爾黑洞6174,到達這個黑洞最多需要14個步驟。
例如:
大數:取這4個數字能構成的最大數,本例為:4321;
小數:取這4個數字能構成的最小數,本例為:1234;
差:求出大數與小數之差,本例為:4321-1234=3087;
重複:對新數3087按以上算法求得新數為:8730-0378=8352;
重複:對新數8352按以上算法求得新數為:8532-2358=6174;
結論:對任何只要不是4位數字全相同的4位數,按上述算法,不超過9次計算,最終結果都無法逃出6174黑洞;
比起123黑洞來,6174黑洞對首個設定的數值有所限制,但是,從實戰的意義上來考慮,6174黑洞在信息戰中的運用更具有套用意義。
設4位數為 XYZM,則X-Y=1;Y-Z=2;Z-M=3;時,永遠出現6174,因為123黑洞是原始黑洞,所以……
自冪數
除了0和1自然數中各位數字的立方之和與其本身相等的只有153、370、371和407(此四個數稱為“水仙花數”)。例如為使153成為黑洞,我們開始時取任意一個可被3整除的正整數。分別將其各位數字的立方求出,將這些立方相加組成一個新數然後重複這個程式。
冰雹猜想(角谷猜想)
冰雹猜想來歷
1976年的一天,《華盛頓郵報》於頭版頭條報導了一條數學新聞。文中記敘了這樣一個故事:
70年代中期,美國各所名牌大學校園內,人們都像發瘋一般,夜以繼日,廢寢忘食地玩弄一種數學遊戲。這個遊戲十分簡單:任意寫出一個自然數N(N≠0),並且按照以下的規律進行變換:
如果是個奇數,則下一步變成3N+1。
如果是個偶數,則下一步變成N/2。
不單單是學生,甚至連教師、研究員、教授與學究都紛紛加入。為什麼這種遊戲的魅力經久不衰?因為人們發現,無論N是怎樣一個非零自然數,最終都無法逃脫回到谷底1。準確地說,是無法逃出落入底部的4-2-1循環,永遠也逃不出這樣的宿命。
強悍的27
冰雹的最大魅力在於不可預知性。英國劍橋大學教授John Conway找到了一個自然數27。雖然27是一個貌不驚人的自然數,但是如果按照上述方法進行運算,則它的上浮下沉異常劇烈:首先,27要經過77步驟的變換到達頂峰值9232,然後又經過32步驟到達谷底值1。全部的變換過程(稱作“雹程”)需要111步,其頂峰值9232,達到了原有數字27的342倍多,如果以瀑布般的直線下落(2的N次方)來比較,則具有同樣雹程的數字N要達到2的111次方。其對比何其驚人!
但是在1到100的範圍內,像27這樣的劇烈波動是沒有的(54等27的2的次方倍數的數除外)。
驗證規律
經過遊戲的驗證規律,人們發現僅僅在兼具4k和3m+1(k,m為自然數)處的數字才能產生冰雹猜想中“樹”的分叉。所以在冰雹樹中,16處是第一處分叉,然後是64……以後每隔一節,產生出一支新的支流。
自從Conway發現了神奇的27之後,有專家指出,27這個數字必定只能由54變來,54又必然從108變來,所以,27之上,肯定可以出現不亞於2n的強大支流——33×2n(n=1,2,3……),然而,27到4-2-1數列和本流2到4-2-1數列要遙遠的多。按照機械唯物論的觀點,從27開始逆流而上的數列群才能叫做本源,儘管如此,按照“直線下瀉”的觀點,一般依然把1-2-4-8……2n的這一支看作是“幹流”。
又稱為角谷猜想,因為是一個名叫角谷的日本人把它傳到中國。
數列驗證法,此方法是根據冰雹猜想的驗證規則而建立的一種驗證方法,是以無限的數列來對付無限的自然數。不管是等差的還是變差的,都是可以直接帶進去計算的 首項差是偶數,那么數列上的所有自然數都是偶數,全體數列除於2,如果首項是奇數公差是偶數,那么數列上全體自然數都是奇數,全體乘上3再加1。如果公差是奇數,首項也是奇數,那么第奇數項必定都是奇數則乘上3再加1,第偶數項必定都是偶數,則除於2。如果公差是奇數,首項是偶數,那么第奇數項必定都是偶數,則除於2,第偶數項必定都是奇數,則乘上3再加1。按照這樣的計算規則計算下去,會遇到許多新的問題,考驗驗證者的智商。比如偶數的通項公式是2n,因為都是偶數所以除於2,得到n,這就是自然數。
按照忽略偶數不記錄的驗證方法進行驗證,第一個被驗證的奇數有可能是能被3整除的奇數,也有可能是不能被3整除的奇數。但是所到達所歸結的第二個奇數,以及第三個奇數(假設存在),整個過程所到達所遇到所歸結所訪問到的每一個奇數,必定都不能再被3整除了。如果都從從能被3整除的奇數開始驗證,路徑上所遇到所歸結的所到達所訪問到的每一個奇數都必定不能再被3整除了,最終都能歸結於1,那么必定遍歷所有的奇數(遍歷是離散數學的概念)。如果都從不能被3整除的奇數開始驗證,那么路徑上所遇到所到達所歸結的所訪問到的每一個奇數必定都不可能再被3整除了,最終都歸結於1(等於說是漏下能被3整除的奇數沒有被驗證)。所以在順向的冰雹猜想驗證過程中,可以把能被3整除的奇數都命名為最起始點的奇數,1是終止點的奇數,而在逆向的冰雹猜想驗證過程中則是相反的,1是最起始點的奇數,而能被3整除的奇數則是終止點的奇數。事實上在驗證的過程中,不能被3整除的奇數,都在存在數量無窮多的上一步的奇數,占1/3的比例是能被3整除的奇數,占2/3的比例是不能被3整除的奇數,這一現象都跟自然數的情況出奇地巧合了.這一規律,無論是單個奇數的驗證方法,還是數列驗證法必須遵守。在能被3整除的奇數之前的,只有能被3整除的偶數,沒有任何奇數。最起始點的奇數在15 x-7 或者是在7x-5的時候就不是能不能被15整除或者被7整除這么簡單了..........
存在X1,使得X1*3+1之後只能被1個2整除,之後就是奇數,這一類奇數占奇數總量的1/2;
存在X2,使得X2*3+1之後只能被2個2整除,之後就是奇數,這一類奇數占奇數總量的1/4;
存在X3,使得X3*3+1之後只能被3個2整除,之後就是奇數,這一類奇數占奇數總量的1/8;
..........
以此類推............從逆推定理出發,可以很方便地找到,X1,X2,X3,X4,X5.........的通項公式
7X-3的平衡點是:
當N=2個未知數的時候
3*(4+7)=7^2-4^2
假設當 N+1= K的時候也是相等的 就是
3*(4^(K-1)+7*4^(K-2)+7^2*4^(K-3)+...........+7^(K-3)*4^2+7^(K-2)*4+7^(K-1))=7^K-4^K
然後再討論:當 K=K+1的時候能不能相等 ,這個問題我算過了, 是成立的。
導致奇數在驗證過程中爬升的本質就是以3換2,而下降的原因就在於只剩最後一個2了時候,........
卡普雷
簡介
取任何一個4位數(4個數字均為同一個數字的例外),將組成該數的4個數字重新組合成可能的最大數和可能的最小數,再將兩者的差求出來;對此差值重複同樣的過程(例如:開始時取數8028,最大的重新組合數為8820,最小的為0288,二者的差8532。重複上述過程得出8532-2358=6174),最後總是達到卡普雷卡爾黑洞:6174。稱之“黑洞”是指再繼續運算,都重複這個數,“逃”不出去。把以上計算過程稱為卡普雷卡爾運算,這個現象稱歸斂,其結果6174稱歸斂結果。
一,任意N位數都會類似4位數那樣歸斂(1、2位數無意義) . 3位數歸斂到495; 4位數歸斂到6174; 7位數歸斂到唯一一個數組(8個7位數組成的循環數組______稱歸斂組);其它每個位數的數歸斂結果分別有若干個,歸斂數和歸斂組兼而有之(如14位數____共有9×10的13次方個數____的歸斂結果有6個歸斂數,21個歸斂組).
一旦進入歸斂結果,繼續卡普雷卡爾運算就在歸斂結果反覆循環,再也“逃”不出去。
歸斂組中各數可以按遞進順序交換位置 (如a → b → c 或 b → c → a 或c → a → b)
歸斂結果可以不經過卡普雷卡爾運算就能從得出.
某個既定位數的數,它的歸斂結果的個數是有限的,也是確定的.
二,較多位數的數(命它為N)的歸斂結果是由較少位數的數(命它為n,N﹥n)的歸斂結果,嵌加進去一些特定的數或數組而派生形成. 4、6、8、9、11、13的歸斂結果中的8個稱基礎數根.它們是派生所有任意N位數的歸斂結果的基礎.
分類
1,嵌加的數分三類。
第一類是數對型,有兩對:1)9,0 2)3,6
第二類是數組型,有一組:
7,2
5,4
1,8
第三類是數字型,有兩個:
1) 5 9 4
2) 8 6 4 2 9 7 5 3 1
2,嵌入數的一部分嵌入前段中大於或等於嵌入數的最末一個數字的後鄰位置。另一部分嵌入後段相應位置_____使與嵌入前段的數形成層狀組數結構。
594隻能嵌入n=3+3k 這類數。如9、12、15、18…….位。
3,(9,0)(3,6)兩對數可以單獨嵌入或與數組型、數字型組合嵌入。
數組
7,2
5,4
1,8
必須“配套”嵌入並按順序:(7,2)→(5,4)→(1,8) ;或 (5,4)→(1,8)→(7,2)
或 (1,8) →(7,2) →(5,4)。
4,可以嵌如一次、二次或若干次 (則形成更多位數的歸斂結果)。
任意N位數的歸斂結果都 “隱藏”在這N位數中,卡普雷卡爾運算只是找出它們而不是新造成它們。
【“6174數學黑洞”現象的參考資料】
1.美國《新科學家》,1992,12,19
2.中國《參考訊息》,1993,3,14-17
3.王景之: ⑴ 也談數學“黑洞”——關於卡普雷卡爾常數。
⑵ 我演算得到的一部分歸斂結果。
4.天山草:能夠進行任意多位數卡普雷卡爾(卡布列克) 運算的程式。
操作演示
上文對6174黑洞運算過程進行了演示,以下用C演示了對任一四位數(不全相同,如2222)計算過程,並總計了一共操作的步驟。編譯連線後,輸入輸出結果如右圖所示: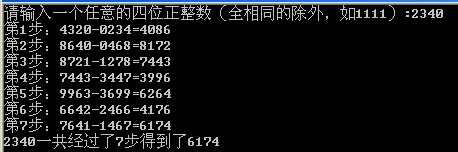 6174黑洞運算操作演示
6174黑洞運算操作演示
 6174黑洞運算操作演示
6174黑洞運算操作演示#include <stdio.h>void insertSort(int r[], int len) { int i, k, tmp; for(i = 1; i < len; i++) { k = i - 1; tmp = r[i]; while(k >= 0 && r[k] > tmp) { r[k+1] = r[k]; k--; } r[k+1] = tmp; }}void main() { int N, count, end, s; int r[4]; int max, min; printf("請輸入一個任意的四位正整數(全相同的除外,如1111):"); scanf("%d", &N); count = 0; end = 0; s = N; while (end != 6174) { r[0] = s % 10; r[1] = s / 10 % 10; r[2] = s / 100 % 10; r[3] = s / 1000; insertSort(r, 4); max = 1000 * r[3] + 100 * r[2] + 10 * r[1] + r[0]; min = 1000 * r[0] + 100 * r[1] + 10 * r[2] + r[3]; end = max - min; count++; printf("第%d步:%d-%d=%d\n", count, max, min, end); s = end; } printf("%d一共經過了%d步得到了6174\n", N, count);}
