衡齋算學(Hengzhdi sudnxu的清代數學家汪萊的數學著作集.七冊.《衡齋算學》第一冊(1796)和第四冊(1798)前半是汪萊對球面三角形的討論.
基本介紹
- 書名:古籍名:衡齋算學遺書合刻
- 作者:(清)汪萊
- 類別:版 本:刻本
- 出版社:聞梅舊塾,
衡齋算學(Hengzhdi sudnxu的清代數學家汪萊的數學著作集.七冊.《衡齋算學》第一冊(1796)和第四冊(1798)前半是汪萊對球面三角形的討論.
第一冊系統討論了球面三角形有解、無解的條件.對自由球面三角形,已知兩邊及其一對角或兩角及其一對邊的求解,各列出26種情形討論.對球面直角三角形,討論了9種有解的情形並給出具體解法.對於已知球面三角形邊角六元素中任意三個,求其餘元素,共有六種情形.第四冊就六種情形給出有解的充分條件.汪萊對方程論的研究見於《衡齋算學》第二冊(1798)、第五冊(1801)和第七冊(1805).
在第二冊中,汪萊指出形如.}(p-.}>2=q的方程可有二正根,其中p>O,q>O,OG.}Gp.在該問題的研究中,汪萊還給出了等勾弦和兩勾股形等積的充分必要條件.第五冊系統討論有實根的二次方程和三次方程正根的個數,無正根的情形不予討論.本冊按照方程係數的符號列舉96條,歸納之後,共是16個方程. 凡方程有一正根者稱為可知,多正根者稱為不可知,有一正根或多正根者稱為可知或不可知.對最後一種情形,汪萊給出判別方法.第七冊討論有實根的高次方程正根個數的出現規律和正根的判別條件,無實根的情形不予討論.本冊提出了方程的分類,以舉例方式顯示正根出現規律,說明正根的判別條件,給出方程x"-px'"+q=0 (n,m是正整數,nom,p}0,q}0)有正根的充分必要條件是
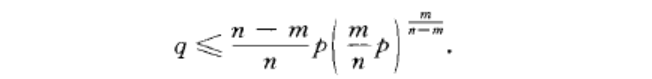
第四冊後半為《遞兼數理》,在此處,汪萊將組合作為一個數學問題第一次予以嚴謹的論述,其中包括組合的定義、計算公式、基本性質和一個組合恆等式.第三冊(1798)和第六冊(1801)討論三角函式表造法,分別給出由本弧通弦求其五分之一弧通弦和由本弧通弦求其三分之一弧通弦的方法.
《衡齋算學》的版本有二冊本(六九書榭,1798年刊於款縣)、六冊續刊本(六九書榭、嘉樹堂,1802年續刊於揚州)、七冊續刊本(六九書榭、嘉樹堂、桂蔭堂,1810年續刊於石棣).現在流傳較多的是《衡齋算學遺書合刻》本,其有鹹豐四年(1854)夏燮都陽縣署刊本和光緒十八年(1892)汪廷棟聞梅舊塾刊本.

