在衝擊載荷下,材料表現出與靜態或準靜態載荷作用時不同的力學性能。在持續短暫時間的強載荷作用下,材料會發生變形和破壞,相應的組織結構和性能也會發生永久性的變化。衝擊載荷下材料的變形行為,表現為變形同應力、應變率(應變隨時間的變化率)、溫度、內能等變數之間的複雜關係,包括屈服應力(見屈服條忤)和流動應力的應變率致應、溫度效應及應變率的歷史效應等等。
基本介紹
- 中文名:衝擊載荷下材料的力學性能
- 外文名:Mechanical properties of materials under impulsive load
概述,高速衝擊載荷下材料變形的描述,中低速衝擊載荷下材料變形的描述,應變率和溫度效應,本構方程,動態破壞現象,絕熱剪下帶,崩落,動態脆性,遺留效應,
概述
在持續短暫時間的強載荷作用下,材料會發生變形和破壞,相應的組織結構和性能也會發生永久性的變化。衝擊載荷下材料的變形行為,表現為變形同應力、應變率(應變隨時間的變化率)、溫度、內能等變數之間的複雜關係,包括屈服應力(見屈服條忤)和流動應力的應變率致應、溫度效應及應變率的歷史效應等等。描述這種關係可用高壓固體狀態方程和各種本構方程(見本構關係)。在衝擊載荷的作用下,材料有多種動態破壞形式,主要表現在以下幾個方面:①局部大變形;②溫度效應引起的絕熱剪下掖壞;③應力波相互作用造成的崩落破壞;④應變率效應引起的動態脆性。這幾方面的力學性能都以各種時效、熱與機械功的耦合以及有限的體積變形和塑性畸變為特徵,這些特徵有時是同時存在的,有時則某一點更為突出。衝擊載荷在材料中引起的微觀組織的特殊變化(如動態相變等,有些是不可逆的,在載荷去掉之後,對材料的力學性能仍然有明顯的影響,這種現象稱為衝擊載荷的遺留效應。
機械碰撞掩和各種形式的爆炸載荷是最常見的衝擊載荷。它們的強度一般至少都足以引起材料的塑性變形,而載荷持續的時間則從納秒(如薄膜的撞擊和輻射脈衝載荷)、毫秒至秒(如核爆炸或化學爆炸對結構物的載荷)的量級。通常根據受衝擊載荷作用的材料的質點速度v和特徵強度(如屈服應力σy)將衝擊載荷分為低速、中速、高速三種,受衝擊載荷作用的材料特性也相應地分為三種:
①低速衝擊載荷ρυ/σy約為10~10(ρ為材料的密度)。介質變形量不大,以時效現象為主,可用等溫近似方法處理。
②中速衝擊載荷ρυ/σy約為10〜10。介質發生有限彈塑性變形,時效、熱與機械功的耦合都比較明顯,體積可壓縮性也需要考慮,相應地有各種描述變形過程的本構關係。
③高速衝擊載荷ρυ/σy約為10〜10。與材料強度有關的諸效應退居次要地位,而以體積壓縮變形和熱的耦合為主要特徵。介質變形可按照可壓縮流體處理,其變形行為可用各種高壓狀態方程描述。
高速衝擊載荷下材料變形的描述
材料在高速衝擊載荷下的變形行為,通常用以內能、體積和壓力為參量的高壓固體狀態方程描述。這種方程反映固體在大體積變形的情況下體積變形功和固體內能(物質結構勢能和熱振動能)之間的關係。米-格呂內森方程是最常用的高壓固體狀態方程:
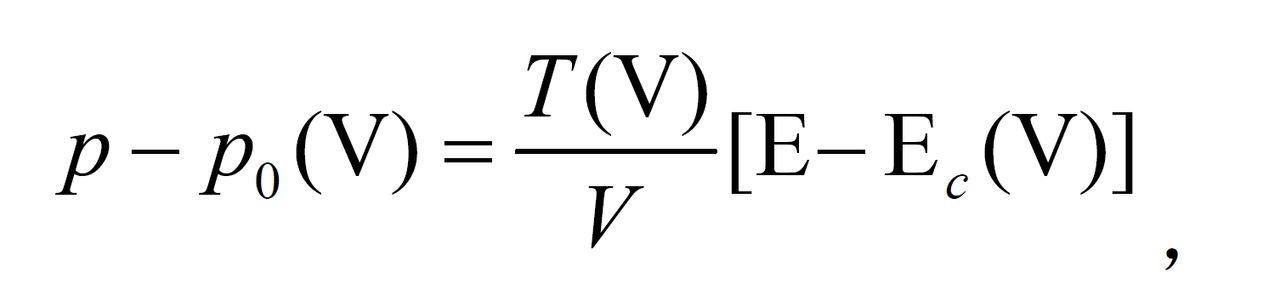
式中p為壓力;V為體積;E為內能;T為格呂內森係數; 為“冷”壓;Ec為“冷”內能,反映晶體點陣的勢能。該方程適用於力
為“冷”壓;Ec為“冷”內能,反映晶體點陣的勢能。該方程適用於力 帕。在更高的壓力下,不同物質的結構(如點陣)已不存在,物質成為某種統一的狀態(如電子-核體系)。適用於這種情況的狀態方程有托馬斯-費密方程(TF方程)和托馬斯-費密-狄喇克方程(TFD方程)等。
帕。在更高的壓力下,不同物質的結構(如點陣)已不存在,物質成為某種統一的狀態(如電子-核體系)。適用於這種情況的狀態方程有托馬斯-費密方程(TF方程)和托馬斯-費密-狄喇克方程(TFD方程)等。


在爆炸力學中還常用許多經驗性的高壓固體狀態方程,適用於和米-格呂內森方程相仿的壓力區間,如蒂洛森方程:
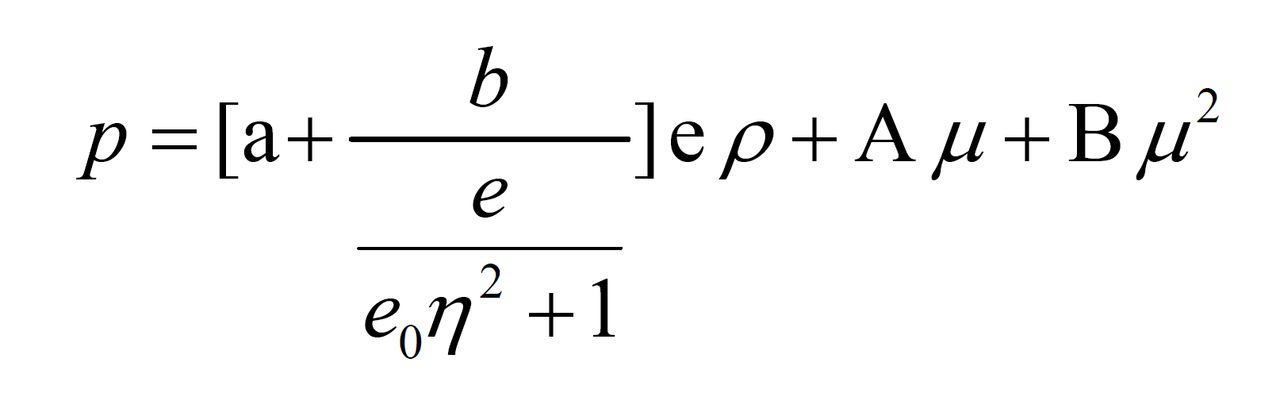
式中η=μ+1=ρ/ρ0;ρ和ρ0分別為初始密度和密度;e為比內能(單位質量物質的內能);e0為物質常數;a、b、A、B為實驗參量(見表1)。
表3某些材料的實驗參量
鋼 | 鋁 | 鈹 | |
ρ0(克/厘米) | 7.8 | 2.79 | 0.845 |
e0(爾格/克)* | 9.5×10 | 5×10 | 17.5×10 |
a | 0.5 | 0.5 | 0.55 |
b | 1.5 | 0.63 | 0.62 |
A(達因/厘米) | 1.28×10 | 0.75×10 | 117×10 |
B(達因/厘米)* | 1.05×10 | 0.65×10 | 0.55×10 |
*1爾格=10焦耳;1達因=10牛頓。
中低速衝擊載荷下材料變形的描述
在中、低速衝擊載荷作用下材料的變形行為主要涉及應變率和溫度效應,對變形行為的描述有各種形式的本構方程。
應變率和溫度效應
在中、低速衝擊載荷作用下,材料不同程度地表現出各種時效,主要是應變率效應。高應變率效應往往相當於低溫效應。常用一個溫度和應變率組合而成的參量(Z-H參量)Tln(K/έ)來表示溫度T和應變率έ對應力-應變關係、屈服應力和流動應力產生的綜合效應(K為材料常數)。分述如下:
①屈服應力的應變率效應和溫度效應
屈服應力隨Z-H參量增大而降低。在高應變率條件下,會發現載荷雖已超過屈服應力,但屈服現象並不立即出現,如碳鋼的塑性變形可滯後幾十微秒才發生,這稱為屈服滯後。
②流動應力的應變率效應和溫度效應
在應變率έ為10〜10秒的範圍內,流動應力大致隨應變率的對數呈線性變化。參量
—般隨溫度和應變的增大而增大。對於大多數金屬,λ的範圍約為10〜10帕。如鉬約為7×10帕,鈹為18×10帕,鈦合金約為50×10帕。在 =10秒處,多數金屬材料的流動應力隨應變率的提高而劇增。
=10秒處,多數金屬材料的流動應力隨應變率的提高而劇增。

③應變率歷史效應
表示材料對過去應變率歷史不會立即“忘卻”。如在剪應變率 發生跳躍(由
發生跳躍(由 跳到
跳到 )的實驗中,跳躍後的應力-應變曲線並不立即與恆定
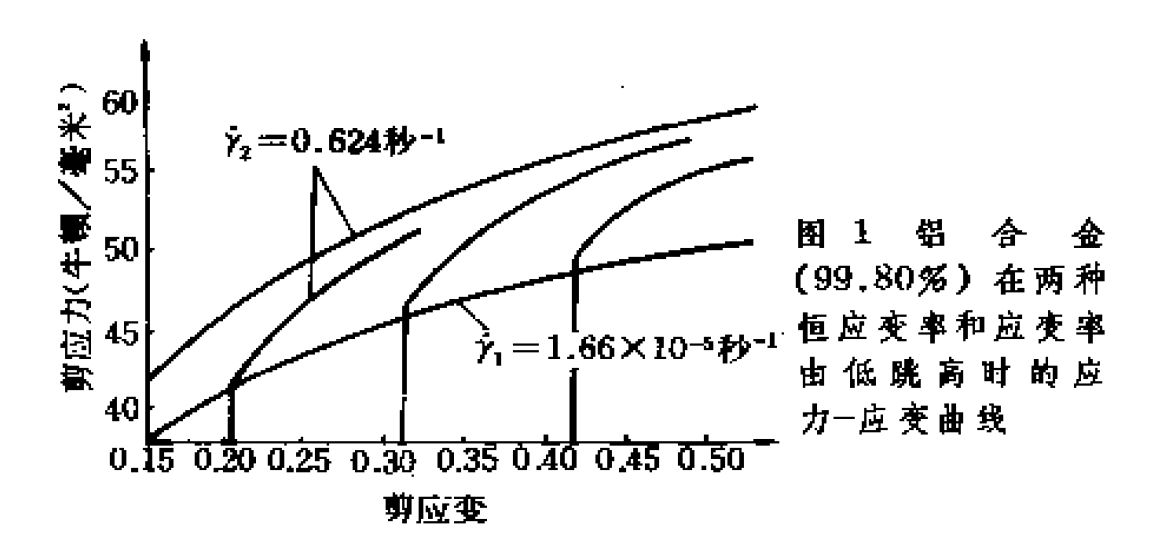
)的實驗中,跳躍後的應力-應變曲線並不立即與恆定 條件下的曲線重合。圖1給出三個實驗中剪應變率發生跳躍時的應力-應變曲線,當剪應變達到約0.21(0.32、0.42)時,剪應變率
條件下的曲線重合。圖1給出三個實驗中剪應變率發生跳躍時的應力-應變曲線,當剪應變達到約0.21(0.32、0.42)時,剪應變率 從突然跳到
從突然跳到 ,這時的應力-應變曲線與恆定
,這時的應力-應變曲線與恆定 條件下的曲線不重合。
條件下的曲線不重合。







④彈性前驅波的波幅衰減和應力鬆弛
彈性前驅波就是一維應變下的彈性縱波,它本應以恆速、恆幅向前傳播。衝擊實驗發現,彈性前驅波雖然是恆速,但波幅卻隨傳播距離而衰減,而且在波峰後,有一段應力下降(鬆弛),然後才出現高幅度的塑性波。圖2中不同位置和時刻的應力波形,表明彈性前驅波的波蝠衰減和應力鬆弛。
這些都與波陣面上較大的塑性畸變密切相關。目前用位錯運動的微觀模型可以解釋並計算模擬上述現象。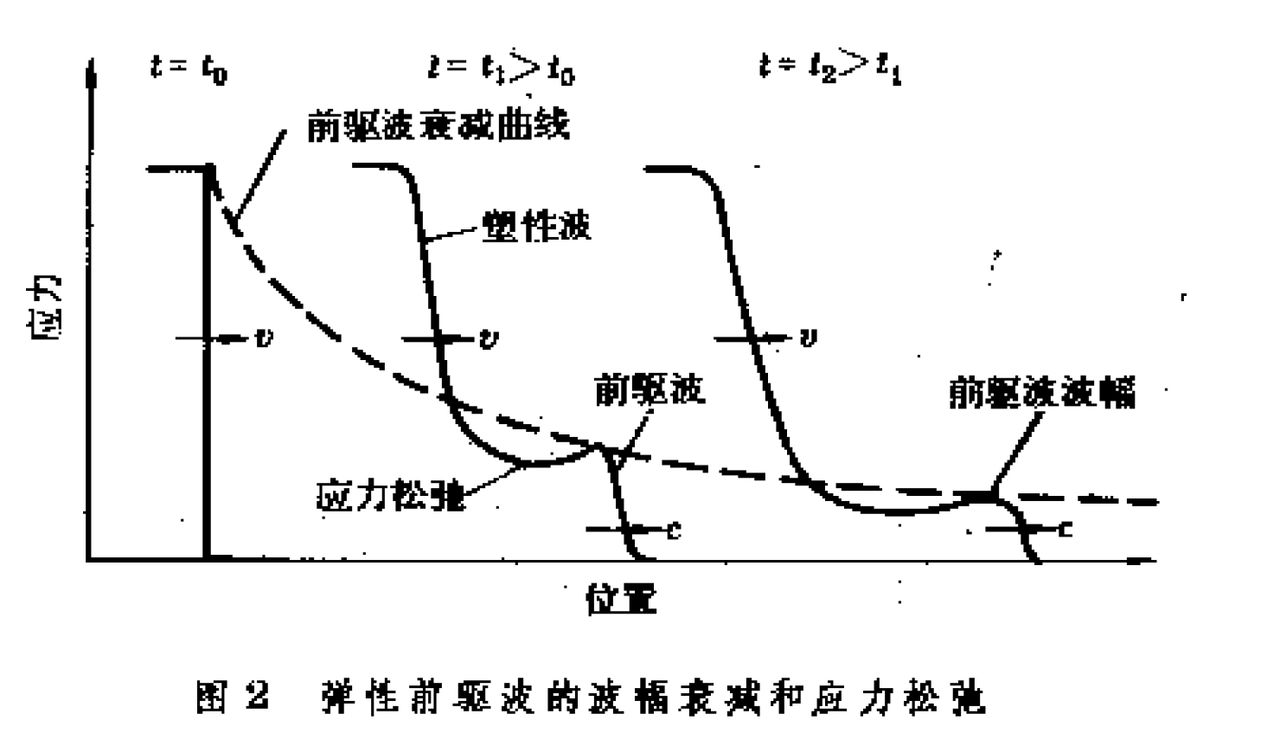

本構方程
這裡研究的本構方程是指材料在中、低速衝擊載荷作用下,變形過程中諸力學量(例如應力和應變)相互關係的物性方程。根據中、低速衝擊載荷下材料變形的種種現象,本構方程應能包括應變率、溫度、變形歷史(包括應變和應變率歷史)等等,從而能綜合描述各種時效以及有限變形效應。但目前還沒有一個本構方程能夠概括所有這些效應。常見的本構方程有:
①索科洛夫斯基-馬爾文方程:
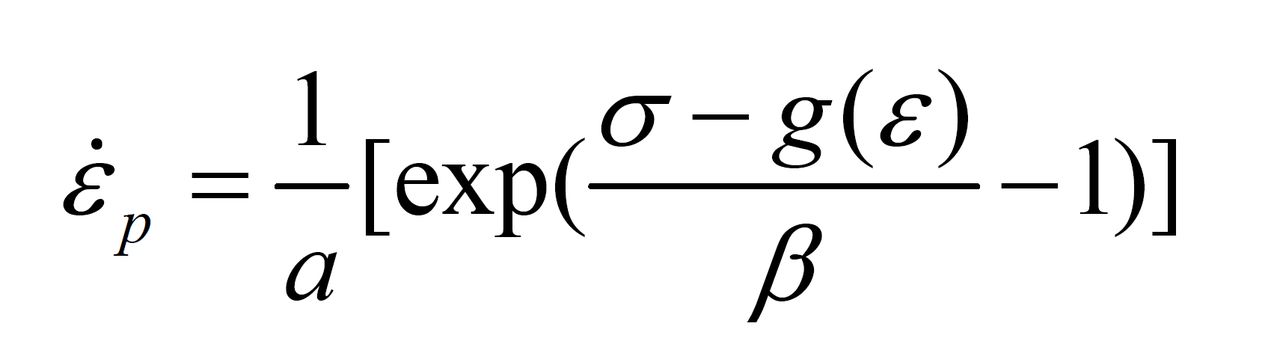
式中 為塑性應變率;g(ε)為準靜態應力;α和β為特定常數。這是一個一維的率型方程。型性應變率反映為過應力σ-g(ε)的粘性。
為塑性應變率;g(ε)為準靜態應力;α和β為特定常數。這是一個一維的率型方程。型性應變率反映為過應力σ-g(ε)的粘性。

②奧羅萬-吉爾曼方程;
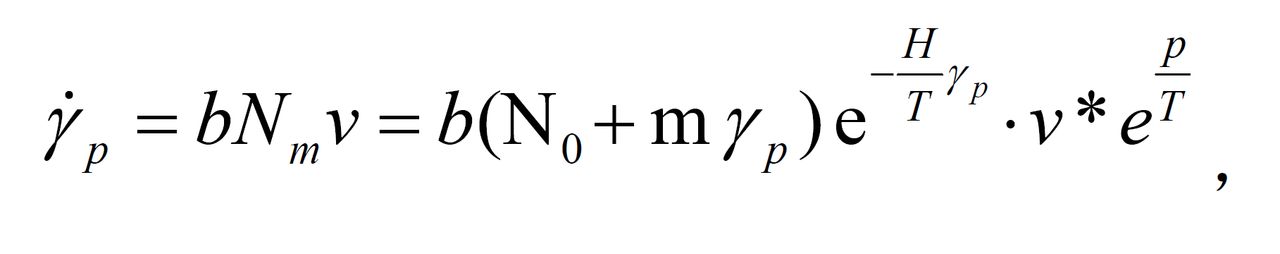
式中 和
和 分別為塑性剪應變和塑性剪應變率;b為伯格斯矢量的大小;N0和Nm分別為初始位錯密度和可動位錯密度;υ和υ*分別為平均位錯速度和極限位錯速度;m為位錯增殖密度;T為剪應力;D為位錯的特徵阻滯應力;H為應變強化係數。這是基於位錯理論的本構方程。
分別為塑性剪應變和塑性剪應變率;b為伯格斯矢量的大小;N0和Nm分別為初始位錯密度和可動位錯密度;υ和υ*分別為平均位錯速度和極限位錯速度;m為位錯增殖密度;T為剪應力;D為位錯的特徵阻滯應力;H為應變強化係數。這是基於位錯理論的本構方程。


③佩日納方程:
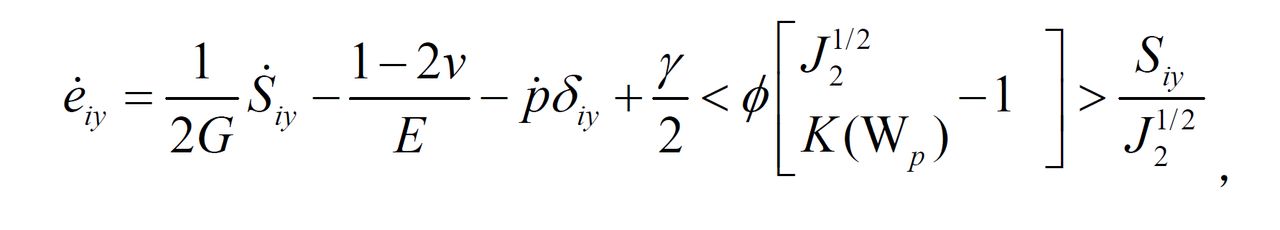
其中
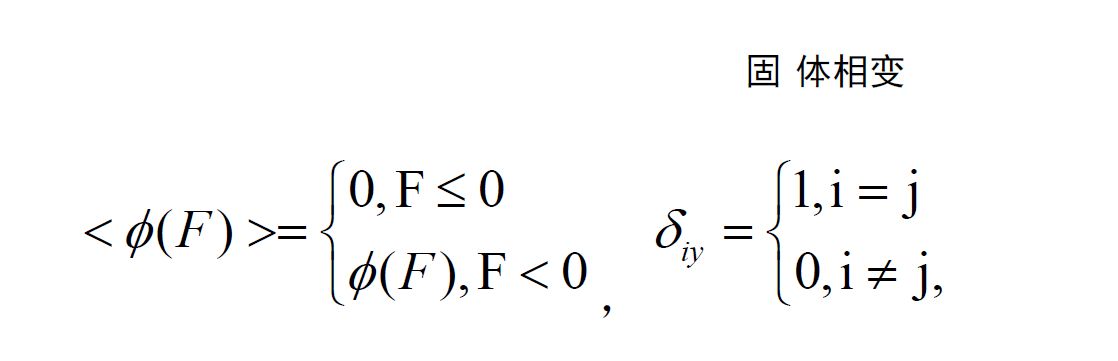
式中 為應變率偏量;
為應變率偏量; 和
和 分別為應力偏量和應力偏量速率;
分別為應力偏量和應力偏量速率; 為靜水壓力速率;J2為應力偏量第二不變數;G、E、υ分別為剪下模量,楊氏模量和泊松比;Wp為塑性功;K(Wp)為材料物理狀態的函式;γ為一常數。佩日納方程是索科洛夫斯基-馬爾文方程的三維推廣,但仍只適用於等溫和小應變的情況。
為靜水壓力速率;J2為應力偏量第二不變數;G、E、υ分別為剪下模量,楊氏模量和泊松比;Wp為塑性功;K(Wp)為材料物理狀態的函式;γ為一常數。佩日納方程是索科洛夫斯基-馬爾文方程的三維推廣,但仍只適用於等溫和小應變的情況。




④流體彈塑性本構方程
考慮到衝擊載荷引起的大變形和明顯的熱效應,需要套用流體彈塑性本構方程。對於熱功耦合和大變形的描述是十分困難的。一個大為簡化的描寫方法是,把變形視為形狀變形和體積變形二部分之和。形狀變形部分用小彈塑性本構方程(如普朗特-羅伊斯方程)描寫,而體積變形部分用高壓回體狀態方程描寫。
動態破壞現象
在高速破撞等衝擊載荷作用下引起的大塑性變形,能形成諸如開坑、鼓包等動態破壞形態。此外,還有如下一些特殊的形態。
絕熱剪下帶
受衝擊載荷作用後,在材料發生大塑性變形的區域中,存在一些白色的亮帶,稱為絕熱剪下帶,在壓力加工工藝中則稱為熱線。這是由於在極高的應變率(>106秒-1)下,局部大塑性畸變產生的熱來不及傳輸出去,使變形加劇而形成的。判斷絕熱剪下帶的發生有臨界剪應變準則(如對金屬鈦,臨界剪應變約為1.15)和臨界應變率準則。有時,絕熱剪下帶有裂紋伴生。裂紋可沿絕熱剪下帶發展,也可出現與絕熱剪下帶斜交的多個裂紋(圖3)
崩落
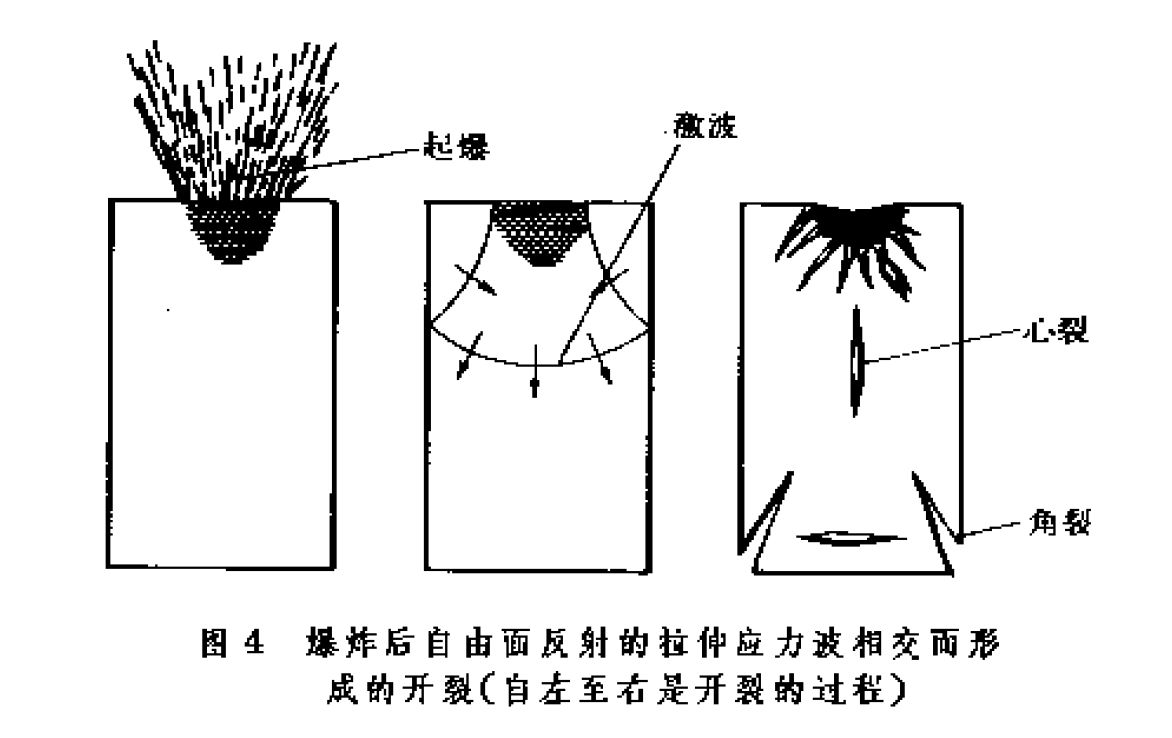
崩落是拉伸應力波造成的材料斷裂。拉伸應力波是從受載面開始的壓應力波在自由表面反射形成的,所以崩落多發生在受衝擊體的背面自由表面附近或拉伸應力波相交而增強的區域(圖4)。崩落破壞面是由許多裂紋或孔洞連線而成的(圖5)。崩落表現出強烈的時效,載荷持續時間越短,達到破壞所對應應力越大。


動態脆性
由於應變率的增大,屈服應力和流動應力相應地提高,使塑性變形區縮小,從而導致材料脆化,表現為材料脆性-韌性轉變溫度的提高和斷裂韌性的下降。
遺留效應
衝擊載荷在固體中造成的瞬時高壓(常伴有高剪應力)、高溫和高應變率,往往造成材料的組織結構和性能的永久變化,這種變化在卸載後依然後存在,稱為遺留效應。主要表現為不可逆相變、顯微結構和力學性能的變化。激波在固體中引起的不可逆相變見表2。
表2激波在固體中引起的不可逆相變
固體相變 | 激波壓力 |
石墨和無定形碳→金剛石 | ≈30 |
鈄長石→熔料長石 | 25~30 |
α石英(單晶)→玻璃態 | ≈36,50 |
石英→柯石英 | >15 |
石英→超石英 | >15 |
鈉長石→玻璃態 | >60 |
赤磷→黑磷 | 2.5~3.5 |
黃磷→黑磷 | 7~8 |
奧氏體不鏽鋼:fcc→bcc* | 15~35 |
鐵鎳合金(68/32):bcc→fcc | 17,27 |
鈷:fcc(β)→六方(α) | 7 |
TiO2:金紅石→螢石型 | 25 |
磁鐵礦→赤鐵礦 | 10.5~16.5 |
*fcc為面心立方點陣;bcc為體心立方點陣。
可以利用激波引起的不可逆相變合成新材料(例如用爆炸法人工合成金剛石),也可以作為測量和標定壓力的一種手段(例如利用石英相變來測量爆源附近的壓力範圍)。
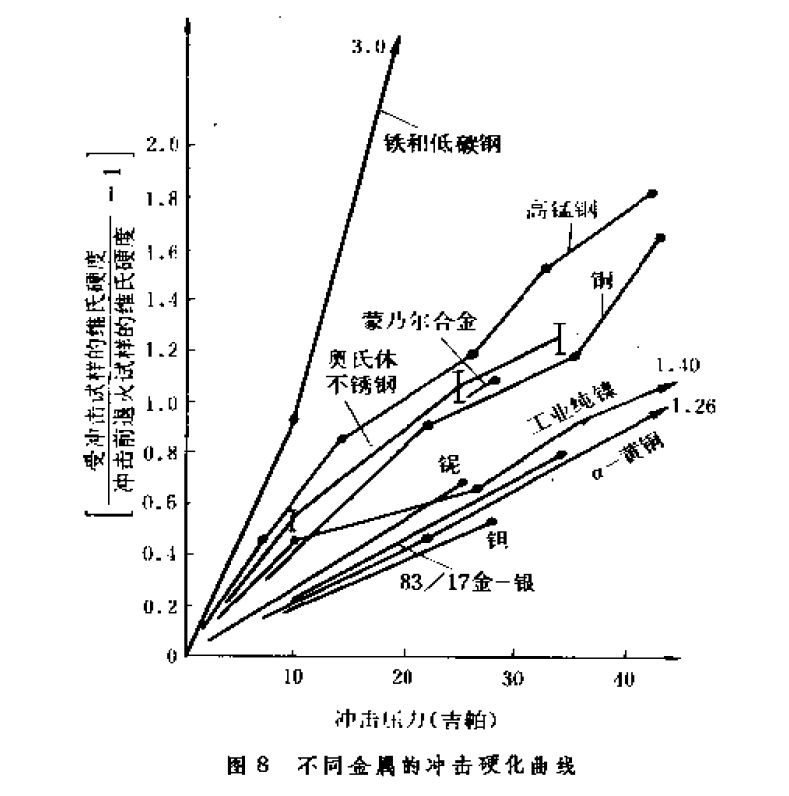
衝擊載入於體心立方金屬,常常產生大量的變形孿晶(圖6)。孿晶的多少同衝擊壓力的大小和持續時間有關。面心立方金屬除在很高的壓力下出現少量孿晶夕卜,一般呈現密集的滑移條紋(圖7),在衝擊載荷作用下,點陣扭曲,位錯密度增大,點缺陷大量增加,這些都使變形材枓的內能增高。組織結構的變化和內能的增加,使變形後材料的硬度和強度比靜態變形後明顯提高。圖8為經不同衝擊壓力作用後材料硬度的變化曲線。但如果壓力過大,熱效應的作用會使硬度降低,例如鎳和奧氏體不鏽鋼在10〜15吉帕時即顯示出回軟現象。與硬度直接有關的是材料的強度,隨硬度的提高,材料的強度亦相應增大。至於衝擊載入之後,材料的疲勞性能、抗應力腐蝕性能和衝擊韌性值是否降低,延脆性轉變溫度是否提高等等,至今還沒有得出一致的結論。


在生產上,高錳鋼爆炸硬化和奧氏體反磁鋼的爆炸強化已經廣泛套用。經過激波載入然後進行再結晶退火能使材料的晶粒細化,塑性增加,低溫脆性和高溫蠕變性能改善。在常規形變熱處理的基礎上,正在發展一種衝擊形變熱處理方法。這是利用衝擊載荷遺留效應的一個有發展前景的途徑,但是還沒有達到工業上套用的程度。
