行星引力輔助變軌是指從一個星球發射的太空飛行器飛近另外一個星球（行星），利用此星球的引力改變軌道, 向另外的目標星球飛去。這種利用行星引力進行變軌的方式有人將其稱之為借力飛行或近旁轉向技術，也有人將其稱之為引力甩擺或行星引力輔助軌道轉移技術 。
行星引力輔助變軌可更細地劃分為：把探測器非常接近星體的過程叫做飛越(Fly by)或近旁轉向(Swing by)；利用近旁轉向使探測器產生期望的軌道改變效果叫做引力輔助(Gravity assist)。
通過行星引力輔助變軌既可以改變太空飛行器軌道的方向 ,還能使太空飛行器加速或減速 。對於需要很大能量的行星際探測；可以在中途通過行星引力輔助變軌利用某星球的引力獲得速度增量, 從而節省一定的燃料。
基本介紹
- 中文名：行星引力輔助變軌
- 外文名：Planetary gravity assist maneuver
- 又稱：近旁轉向、引力甩擺
- 所屬領域：航空航天
- 基本釋義：利用行星引力輔助太空飛行器改變軌道
- 套用：外太空探測
歷史發展,基本原理,基本特性,軌道模型,軌道設計,
歷史發展
利用行星引力輔助變軌是國際深空探測中常用的技術，例如伽利略號和卡西尼探測器就多次利用地球、金星、木星等改變軌道增加能量，從而節省大量燃料。俄羅斯為了減少高緯度發射地球同步衛星所耗費的燃料，提出利用月球引力輔助變軌的發射方案。而在1998年6月，美國休斯公司利用月球引力成功的挽救了未入軌的亞洲3號地球同步軌道衛星。
使用借力飛行方案探測太陽系中的天體，借力星體無非就是地球的天然衛星(月球)和比所要探測行星離地球更近的太陽系行星。
從火星探測借太陽系行星的引力飛行來看，套用最多的是金星。而金星為深空探測器提供借力源的實例有：美國的水星探測器Mariner10(水手10號)借金星之引力輔助於1974年到達水星；歐空局的Galileo(伽利略號)經過1次金星和2次地球近旁轉向後到達木星；NASA/ESA的聯合項目Cassini(卡西尼號)土星探測器經過了兩次金星近旁轉向於2004年7月到達土星。
基本原理
大多數行星間和行星探測軌道的初步設計基本均從套用圓錐曲線拼接法開始的。在套用這種方法進行軌道設計時，多體問題被分解為一系列的兩體問題。
雅可比(JACOBI)積分
雅可比積分描述了限制性三體問題能量轉移的約束，它是Jacobi在19世紀所發現的。兩個巨大的質量體進行著兩體運動，一個質點在兩個大質量體質心的環繞軌道上運動，此質點的狀態方程將守恆。
蒂塞朗準則(TisserandCriterion)
蒂塞朗是19世紀著名天文學家，他使用Jaco-bi積分來識別彗星，即在限制性三體問題中，彗星軌道要素滿足的某一特定方程在彗星飛越一顆行星前後保持守恆。利用此方程計算兩條不同時期觀察到的彗星軌道並且結果一樣，這可能是同一個彗星在兩次觀察之間飛越了一顆行星，並通過向前或向後推演軌道來確定猜測是否正確。
蒂塞朗準則套用到引力輔助軌道設計中時，設計過程將與彗星識別的過程相反。從發射行星到借力行星並且從借力行星到目標行星的計算可以使用Lambert定理完成，而識別這些軌道的可行性將需要使用蒂塞朗準則。
基本特性
圖1給出了典型的行星引力輔助變軌的兩種視角圖像(行星中心視角和日心視角)。
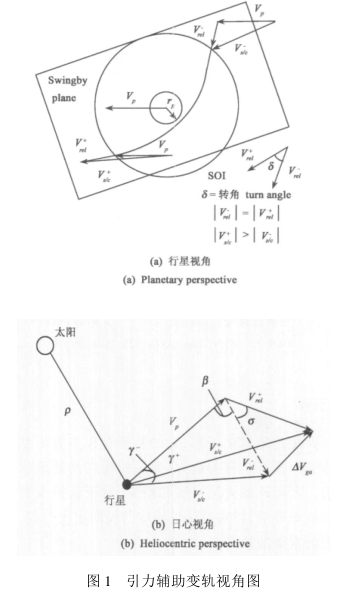
圖1 引力輔助變軌視角圖
圖1中SOI(sphereofinfluence)表示行星的影響球；上標“-”和“+”分別表示探測器飛越行星前後的量；Vrel是探測器相對於行星的速度；V(-)rel表示探測器相對於行星從無窮遠處靠近行星的速度；Vp表示行星的日心速度；Vs/c表示探測器的日心速度；δ表示探測器速度相對行星的矢量在探測器整個近旁轉向其間轉過的角度；γ表示探測器的飛行路徑角；β表示個初始相對速度角(相對於借力行星)；ΔVga表示由於引力輔助影響改變的探測器日心速度；探測器相對於行星的軌道是一條雙曲線，這是因為探器相對於行星的速度大於行星的逃逸速度。
軌道模型
無動力引力輔助模型
在初步軌道設計時，無動力引力輔助（Unpowered Gravity ASSIST，UPGA）可以近似為日心慣性坐標系中的一個瞬時速度脈衝（無需消耗工質），引力輔助前後探測器的日心慣性坐標系位置沒有變化。
有動力引力輔助模型
有動力引力輔助（Powered Gravity Assist，PGA）軌道，可以看作雙曲線俘獲和逃逸軌道的拼接，並在近行星點處施加一次速度脈衝。
軌道設計
以火星探測器藉助金星引力輔助變軌的軌道設計為例，說明行星引力輔助變軌的軌道設計過程。
借金星引力飛行探測火星的軌道設計過程分三步：(1)地球-金星軌道段；(2)金星-火星軌道段；(3)能量(C3)匹配。即可詳細解釋為在借金星引力的火星探測方案中，可以把探測器的軌道分成兩段，第一段是地球-金星的轉移軌道，通過地球-金星轉移軌道的Pork-chop等高線，可以獲取發射能量要求的地球發射時間和對應到達金星的時間，以及到達金星的能量。第二段金星-火星的轉移軌道段，取前一段到達金星的時間作為第二段的初始時間，然後將火星軌道周期分成等份，求取每一等份末段點的時刻，作為到達火星的時間，然後通過求解朗伯(Lambert)問題得到探測器飛出金星的能量和到達火星的速度。如果探測器飛出金星的能量和探測器到達金星的能量相匹配，那么就可以得到從地球經金星借力到達火星的完整軌道，如果不能匹配，那么需要另外尋找發射機會。
Pork-chop圖是以發射時間和到達時間為坐標的所需發射能量的等高線圖。對於一個發射時間段來說，這個能量等高線圖由無數條直接轉移軌道(如Earth-Venus，Earth-Jupiter等)構成。圖上的每一點都是求解相應的Lambert問題得到的。通過繪製的Pork-chop圖可以尋找發射行星和借力星體、借力星體和目標星體之間可行性軌道。
地球-金星軌道段
為了完成地球-金星的軌道設計，首先要尋找地球到金星的發射時機，此時機可以由地球-金星的Pork-chop圖得到。圖2和圖3分別給出了2022～2023年地球-金星發射與到達的Pork-chop圖。圖2中橫坐標表示從地球發射的時間，縱坐標表示到達金星的時間，金星的星曆選用JPL的DE405星曆。
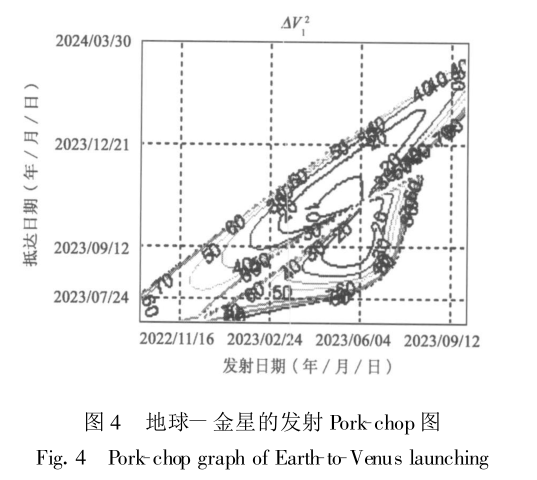
圖2 地球-金星的發射Pork-chop圖
圖3中，等高線表示從地球發射探測器所需要的能量。從能量等高線圖可以看出在等高線的兩個谷底處是發射探測器的最佳時機，因所需的發射能量最少。在2022年10月-2023年10月這段時間內，從地球發射探測器到金星的最佳時間主要集中在2023年4月到6月。在此期間發射探測器所需的能量(兩倍單位質量動能)大約為10(km/s)左右。
圖3表示了2022年10月-2023年10月這段時間內，從地球發射探測器到達金星的到達Pork-chop圖，由此圖可以得到從地球到金星的到達能量，等高線表示到達金星所具有的能量(這裡表示探測器飛越金星時的能量等高線)。此能量將被用來設計近旁轉向期間軌道和下一段的日心軌道，也就是說，這個能量是用於下一軌道匹配的目標能量。
圖3 地球-金星的到達Pork-chop圖
從上圖2與圖3可以看出能量等高線是沿著某一軸不嚴格對稱的，這也證實了短程和長程的能量是非嚴格對稱的。現有火箭的運載能力是有限的，因此這裡選用圖2中滿足現有火箭運載能力的部分發射視窗來進行軌道設計。
金星-火星軌道段
假設探測器進入天體影響球和飛出影響球是同一時刻，將地球-金星軌道段得到的到達金星的日期確定為金星-火星軌道段的發射日期，通過查金星星曆可以得到此時金星的位置。為了設計這段軌道還需要知道到達火星的日期和探測器的飛行時間，對於這段軌道的設計可以通過求解Lambert問題來實現：為了搜尋可行的金星-火星軌道，將火星的軌道周期N等分，對每一個從金星出發的日期，將對應N個抵達火星的日期以及飛出金星時的能量，根據現有運載火箭的運載能力，人為加入發射能量約束(小於35(km/s))，最終得到從金星出發時刻的C3曲線圖(見圖4)。從中可以看出，從金星出發的最佳日期為2023年08月12日-2024年03月06日。
能量匹配
需要將前面兩節設計的兩段軌道拼接起來才能形成完整的借力飛行軌道，這裡採用能量匹配(C3匹配)來完成
C3匹配：飛入金星的能量(目標C3)與飛出金星的能量(C3曲線)匹配。反應在圖8中可以描述為，如果飛入借力天體(金星)的能量(目標C3)與飛出借力天體的能量(C3曲線)有交點，那么表明存在滿足匹配條件的無機動軌道；如果沒有交點，表明在給定時間段內，針對此借力天體，不存在無機動的借力飛行軌道。
使用能量約束(發射能量小於35(km/s))、發射日期約束(2022年10月-2023年10月)和與火星交會時相對速度小於10km/s，可以得到40多組C3曲線(N=T火星/3day)，繪出了幾組典型的仿真圖像，(a)、(b)中C3曲線中是兩條類拋物線，而(c)、(d)中C3曲線中是一條類拋物線。如果在Pork-chop中沿某一橫坐標做垂線，有的發射時刻，對應著4個不同抵達時刻但能量相同的點，而有的發射時刻對應2個能量相同點，這是造成C3曲線有的是兩條類拋物線，有的是一條的原因。需要注意的是C3曲線是加入各種約束後得到的，而Pork-chop圖卻是沒有加入約束得到的，這就會造成對大部分同一出發時刻的同一出發能量(目標C3)，從Pork-chop圖看和C3曲線圖看交點個數不同的原因。如果所加約束更加嚴格，C3曲線將退化為只有一半的類拋物線，這時一個目標C3將和C3曲線只有唯一交點，此交點對應的軌道即為拼接後得到的完整借力飛行軌道。圖5為火星探測以金星借力軌道設計的流程圖。
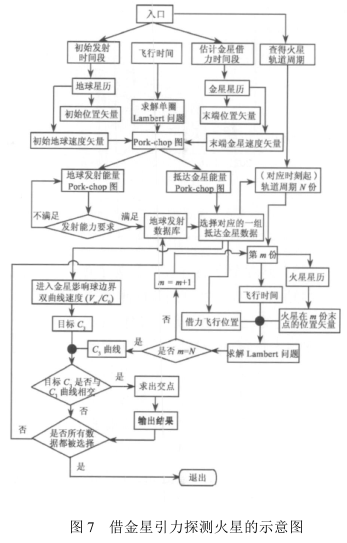
圖5 借金星引力探測火星的示意圖
