引力彈弓效應

引力彈弓效應就是利用大質量的天體會通過引力場捕獲小質量飛行器的特性，實現對小質量飛行器的加速或者減速。利用引力彈弓效應能夠更輕鬆地改變飛行器的軌道，節省燃料。

需要注意的是引力彈弓效應並非局限于飛行器的使用，而是一種自然現象，適用於任何小質量天體利用與大質量天體的引力作用實現加速或者減速的情況。

基本介紹

• 中文名：引力彈弓效應
• 外文名：Slingshot effect
• 定義：利用行星重力場給太空探測船加速
• 用途：把行星當作“引力助推器”

解釋

為了理解引力彈弓，構想一個簡單的物理模型：質量很大的球和質量很小的球發生彈性碰撞。比如一個鉛球和一個桌球碰撞，兩個球都有很好的彈性，碰撞過程不會損失能量。

假如最初鉛球是不動的，桌球以速度撞向鉛球，由於鉛球質量非常大，碰撞後鉛球幾乎還是靜止的。而桌球會發生反彈，並且反彈的時候速度大小還是，保持不變。

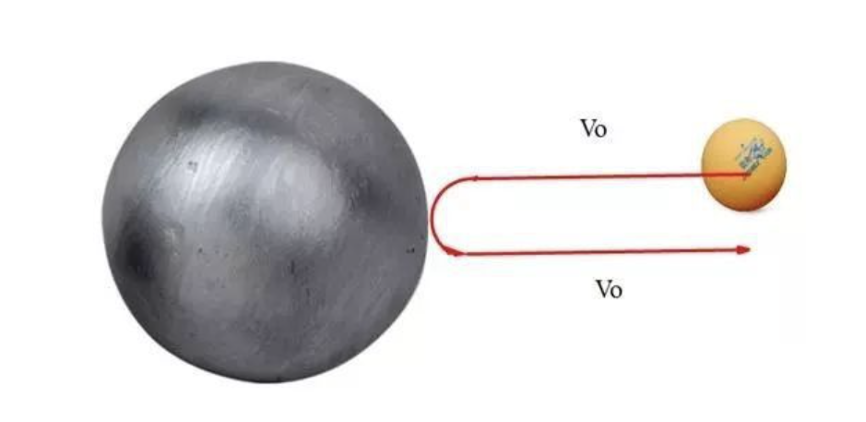
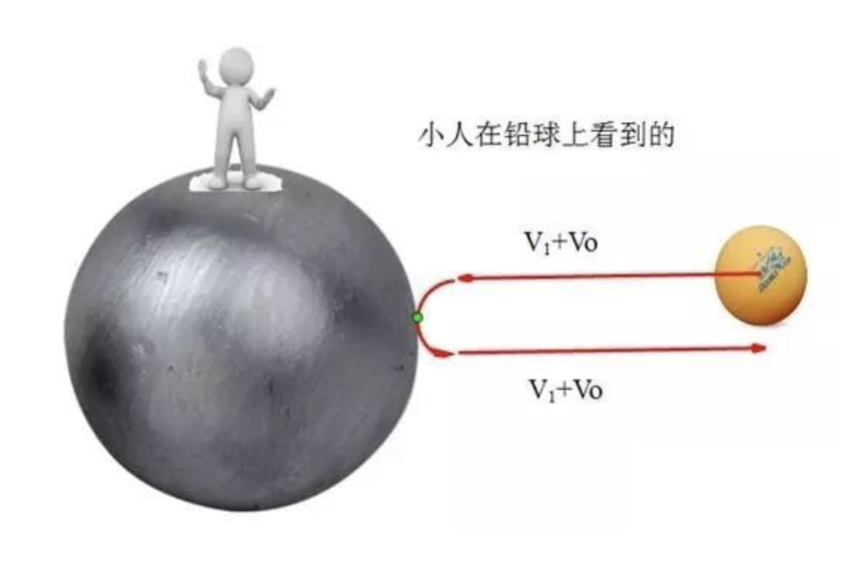
假如最初鉛球是朝向桌球以速度運動，桌球以速度飛來。可以直接由能量守恆和動量守恆解得碰撞後桌球的速度，考慮鉛球質量遠大於桌球的情況，桌球反彈後的速度應為。也可以通過變換參考系求解，首先以鉛球為參考系，桌球向鉛球飛來的速度應為，發生碰撞後桌球速度方向相反，大小不變，仍為。

此時切換為地面參考系，桌球的速度為桌球相對鉛球的速度加上鉛球的速度，因此桌球反彈後離開鉛球的速度為。

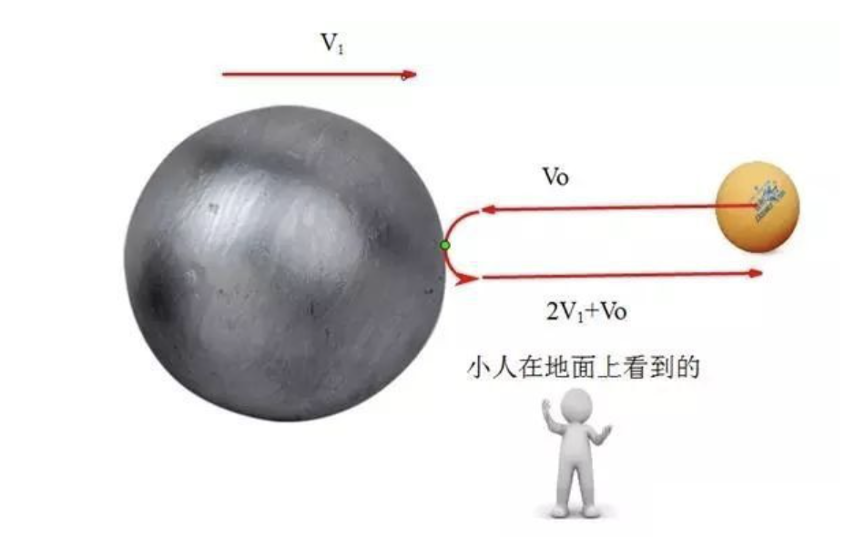
飛行器利用引力彈弓效應加速的過程與桌球和鉛球的碰撞過程類似，只不過飛行器並沒有與行星發生碰撞，而是通過萬有引力實現能量的交換。

由於未考慮軌道的各種細節，所以這是一個過於簡單化的模型。但是如果飛行器沿雙曲線軌道運行，則其無需啟動引擎即可從相反方向離開行星，同時只要其脫離了該行星引力的控制，那么它就可以獲得兩倍行星速度的增量。當然，在實際情況中，由於飛行軌道以及其他因素影響，加速效果並不能達到理想的兩倍行星速度。

在這裡行星的質量遠遠大于飛行器的質量，因此忽略了飛行器對行星速度的影響，而並非是違背了能量守恆和動量守恆定律。

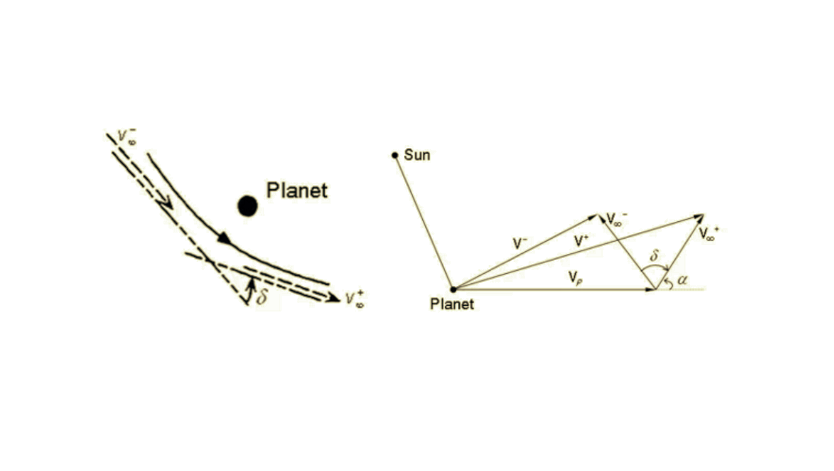
引力彈弓效應速度示意圖

利用引力彈弓效應也可以實現飛行器的減速，加速過程飛行器與行星是“迎面相撞”，減速過程則是飛行器從“背後”追趕上行星，這樣可以實現兩倍行星速度的減速。

分析

在太陽參考系中，行星P的速度為，一飛行器以初速度由無窮遠處的A點進入行星P的引力場範圍，並由無窮遠處的B點離開行星P的引力場範圍。飛行器在行星引力場範圍內運動時，行星對飛行器的引力遠大於太陽對飛行器的引力，飛行器在行星引力場範圍內的運動時間遠小於行星繞日公轉的周期，因此可忽略太陽引力對飛行器和行星組成系統運動的影響，將飛行器和行星視為孤立二體系統。與的夾角為，飛行器相對於行星的初速度，沿方向的直線到行星中心的距離（即瞄準距離）為，飛行器質量為m，行星質量為M，萬有引力常量為G。

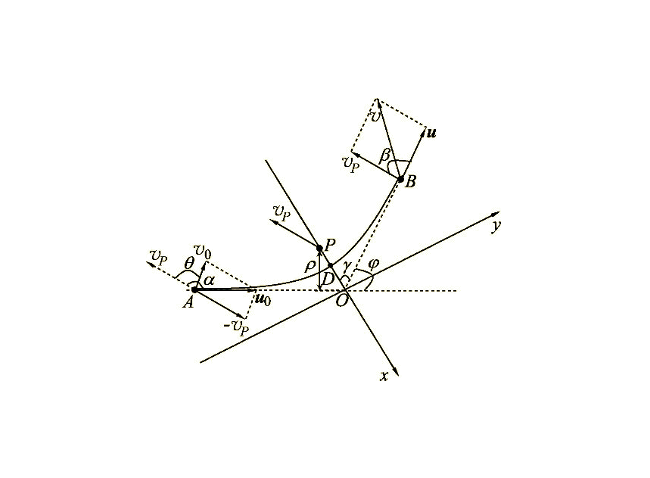
由於行星質量遠大于飛行器質量，可以認為行星的速度保持不變。飛行器在行星引力場中相對行星的運動軌跡是雙曲線，行星P為這支雙曲線相近的焦點。

利用雙曲線幾何性質以及雙曲線軌道能量進行計算，可以得到飛行器在B點離開行星引力場時的速度

其中為與的夾角，為飛行器速度方向偏轉角。

考慮幾種特殊情況。

（1）當飛行器初始速度方向與行星速度方向相反時，末速度大小為

如果瞄準距離為0，此時即是之前描述的理想加速情況，飛行器末速度

（2）當飛行器初始速度方向與行星速度方向相同時，末速度大小為

如果瞄準距離為0，此時即是理想減速情況，飛行器末速度

（3）當飛行器初始速度方向與行星速度方向夾角選取恰當數值時，可以使飛行器離開引力場時的相對末速度方向與同向，即飛行器沿著行星公轉速度的方向離開行星引力場。此時末速度為

意義

引力彈弓效應的意義在於能夠利用更少的燃料實現飛行器的飛行任務，並且通過引力彈弓效應的加速大大縮短飛行任務所需要的時間。

限制

引力彈弓效應最大的限制是用以加速或減速的大質量天體並不總是在理想位置上。以上世紀70年代末發射的旅行者一號、二號飛行器為例，下一次相同的理想時機需要等上176年。

套用舉例

引力彈弓絕對不是只存在於科學家的頭腦和科幻電影之中，而是早已經被人類掌握的空間技術。

最早提出這個技術的人是蘇聯科學家尤里·康德拉圖克, 他在1918年左右發表的論文《致有志於建造星際火箭而閱讀此文者》中提出了引力助推的概念。此人還設計了人類登月的方式，並最終被美國宇航局採納，阿波羅號宇宙飛行器就是基本按照尤里的構想建造的。

不過，引力彈弓的軌道設計需要大量計算，它的正式套用是在大約50年之後。1961年，加州大學洛杉磯分校25歲的研究生麥可·米諾維奇使用當時最先進的IBM7090計算機研究三體問題，順帶計算了一下引力彈弓的軌道。他發現在1970年代末期，太陽系會提供一次絕佳的引力彈弓的機會：木星、土星、天王星、海王星都位於太陽的同一側，如果發射一顆飛行器，依次利用這四顆星球的引力彈弓加速，就可以在12年內，用很少的燃料探訪這四顆星球。如果錯過了這個時機，下次就要再等上176年。NASA利用這次機會開始了航海家號計畫，於1977年NASA發射了旅行者一號和旅行者二號飛行器。如今，兩位旅行者都已經完成了各自的使命，並且已經在宇宙中遨遊了42年，它們已經成功的藉助引力彈弓效應飛到了太陽系的邊緣。

其他飛行器

小行星3753

小行星3753是一顆通過引力助推與地球交換能量，從而周期性改變軌道的近地小行星。

水手10號

水手10號是第一艘藉助引力助推到達另一顆行星的探測器，它於1974年2月5日經過金星，經過引力助推的減速之後到達水星。它是第一艘探測水星的飛行器。

伽利略號

1989年，美國航空航天局通過阿特蘭蒂斯號太空梭在太空中施放了伽利略號探測器。伽利略號最初計畫使用赫曼轉移軌道法，但由於挑戰者號太空梭的事故，伽利略號的“半人馬座”推進火箭不再被允許通過太空梭運至太空，取而代之的是一種功率較小的固態燃料推進火箭。在這種情況下，伽利略號在其軌道上一次飛掠過金星，兩次飛掠過地球，計畫1995年12月到達木星。

伽利略號的工程師調查後認為（但是無法證實）在飛掠過程中飛行器與金星的長時間接觸，使伽利略號上的主天線的潤滑劑失效。該技術故障迫使伽利略號使用功能較差的後備天線。

在其後伽利略號探測木星衛星的過程中，也多次使用引力推進法，從而延長了燃料的使用時間，也增加了其與木星衛星近距離接觸的機會。

尤利西斯號探測器

1990年，歐洲空間局發射了尤利西斯號探測器，用以研究太陽的極地地區。由於太陽系中所有行星的軌道基本上都位於黃道面上，所以為了運動至環繞太陽的極軌道上，該探測器必須將其從環地球軌道上繼承的30千米/秒的速度降為零，同時獲得繞太陽極面運行的軌道速度——但是以現有的太空飛行器推進系統還無法完成該任務。

於是尤利西斯號被發射往木星，當其到達木星“前下方”的一個區域時，即落入了行星的引力場中，之後經歷了1分鐘的引力推進，最終使尤利西斯號的軌道向上彎曲，脫離環木星軌道，進入環太陽的極軌道。這一策略只需足夠尤利西斯號運行至木星的燃料即可。

信使號

信使號飛行器頻繁的使用引力助推來降低速度，最後進入環水星軌道。在其飛行過程中，共一次飛掠過地球，兩次飛掠過金星，三次飛掠過水星，最終將於2011年3月到達水星附近，此時其速度已經降得足夠低，使用剩餘的燃料足以將該飛行器送入環水星軌道。雖然其間的每次飛掠主要都是為了進行引力助推，但是也提供了不可多得的科學觀測機會。

卡西尼號

卡西尼號探測器兩次飛掠過金星，之後又途經地球、木星，最終到達土星。其6.7年的旅程較之霍曼轉移軌道法所用時間——6年稍長，但是所需的速度增量少了2公里/秒，故體積和質量都較大的卡西尼號能夠依靠較少的推進燃料到達土星。赫曼轉移軌道法到達土星所需的加速度總值為15.7公里/秒（此處忽略了地球和土星的引力勢阱以及大氣制動效應），超過了現有飛行器推進系統的推進能力。

羅塞塔號

“羅塞塔”項目是一項里程碑式的大膽探測計畫，其目標是追蹤並最終進入一顆彗星的軌道，隨後向彗星地表釋放一顆著陸器，人類歷史上首次對彗核進行登入探測。其確定的考察目標位木星族彗星67P/丘留莫夫-格拉西緬科彗星。

2004年3月2日，羅塞塔飛行器從南美洲法屬蓋亞那的庫魯航天中心由一枚阿麗安-5型火箭發射升空，隨後進行了3次地球引力彈弓借力和一次火星引力彈弓借力。在其追逐彗星的途中，羅塞塔相繼在2008年和2010年飛越了2867號小行星Steins以及21號小行星Lutetia。2014年8月6日，經過十年追趕，羅塞塔安全進入圍繞目標彗星運行的軌道。2014年11月，羅塞塔在67P彗星上登入。